1. Геометрия
  2. По данным двум сторонам и углу

По данным двум сторонам и углу между ними найдите третью сторону и остальные два угла треугольника: a=8 см, b=15 см, угол гамма=120 градусов

Дашанеси Дашанеси    3   27.02.2019 05:10    2

Ответы
anyamaleva97 anyamaleva97  23.05.2020 15:25

По теореме косинусов найдём CA:

CA^2=a^2+b^2-2*a*b*cos120^{\circ}\\\\CA^2=8^2+15^2-2*8*15*(-\frac{1}{2})\\\\CA^2=64+225+8*15\\\\CA^2=64+225+120=409\\\\CA=\sqrt{409}

Теперь по теореме синусов найдём один из углов, пусть это угол напротив стороны BA , найдём угол C:

\frac{CA}{sinB}=\frac{BA}{sinC}\\\\\frac{\sqrt{409}}{sin120^{\circ}}=\frac{15}{sinC}\\\\\frac{\sqrt{409} }{\frac{\sqrt{3} }{2} }=\frac{15}{sinC}\\\\\frac{2\sqrt{409} }{\sqrt{3} }=\frac{15}{sinC}\\\\\frac{2\sqrt{1227} }{3}=\frac{15}{sinC}\\\\2\sqrt{1227}sinC=45\\\\sinC=\frac{45}{2\sqrt{1227} }\\\\


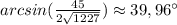
Отсюда ∠C=arcsin(\frac{45}{2\sqrt{1227} })\approx39, 96 ^{\circ}

В сумма углов треугольника = 180°

Найдём ∠A

180^{\circ}-(120^{\circ}+39,96 ^{\circ})=180^{\circ}-159,96^{\circ}\approx20,04^{\circ}



По данным двум сторонам и углу между ними найдите третью сторону и остальные два угла треугольника:
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
homya4okm homya4okm  30.04.2021 11:36
Две прямые касаются окружности с центром О в точках A и B и пересекаются в точке С. Найдите угол между этими прямыми, если AB0=50°.​...
Вика00000011 Вика00000011  30.04.2021 11:37
Терміново!! Знайдіть площу паралелограма якщо його сторони дорівнюють 12м. і 21м. а тупий кут 150 градусів...
Dimas1694 Dimas1694  30.04.2021 11:37
Запишiть рiвняння кола у яке переходить коло (x+1)² (y+1)²=1 При паралельному внесеннi на вектор a(1;‐1).​...
gaiciuknataliaozve2o gaiciuknataliaozve2o  30.04.2021 11:38
Дуже швидко Потрібно зробити номер з контрольної по геометріїТретій​...
thomsonrubi thomsonrubi  30.04.2021 11:38
Скільки осей симетрія має квадрат 6 КЛАСС...
nonyshko nonyshko  03.09.2020 23:17
Если даны точки A(3; -4) и B(-5; 8), Найдите координаты точки N, которая является центром отрезка...
Yoidzokumi Yoidzokumi  07.04.2021 17:46
Дано: правильный четырехугольник, r4=4.Найти: a4, P4, R , S4 Периметр правильного шестиугольника, вписанного в окружность, равен 30 см. Найдите площадь правильного...
Валерушка8 Валерушка8  07.04.2021 17:45
Гомотетія k=3 , очень надо. это рисунок если что​...
qawsed123 qawsed123  16.04.2020 08:26
Решите задачи можете решить 1 задачу на выбор...
orlovski155555 orlovski155555  16.04.2020 08:26
Дерево имеет в обхвате 120 см. найдите примерную площадь поперечного сечения (в см^2), имеющего форму круга( примените пи≈3). Если можно по подробнее. заранее...

Популярные вопросы