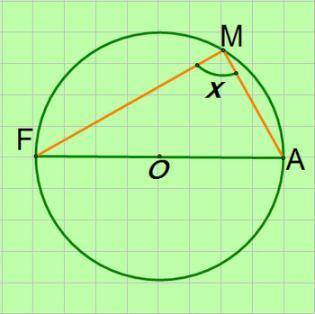
плз решить. 8 класс. Геометрия. Центральные и вписанные углы. О - центр окружности:
Найти:
1. Х;
2. определить вид треугольника FMA (по углам, ответ записать одним словом)
Другие вопросы по теме Геометрия
Популярные вопросы
- В6 ящиков разложили поровну 54 мандаринов. 4 ящика с мандаринами...
2 - Из числа 1 надо получить 100 прибовляя 1(+) и умножая на 2 (*)...
3 - Один пресс делает норму за 4 часа. другой пресс делает норму...
1 - Скаких реакций можно различить анилин, циклогексиламин, n-метиланилин...
1 - Вгороде уфе какие есть места связанные с тематикой вов...
1 - Это присобление поддерживает правую руку живописца при обработке...
3 - Вставте пропущенные буквы и объясните почему пример: к..лометров-...
1 - С! ex.8. change the sentences to use passive structures. example:...
3 - Найти 29-й член арифметической прогрессии (an) первый член который...
3 - Уменя есть стихи подскажите как один из них улучшить его для...
3
1. Найдем значение угла AOM (угол вписанный):
Угол AOM равен половине центрального угла, соответствующего дуге AM. Значит, угол AOM = 1/2 * центральный угол AEM.
Для того чтобы найти центральный угол AEM, нужно заметить, что угол OMA (угол центральный) составляет 360°. Угол AEM равен разности между центральным углом и вписанным углом AOM.
Таким образом, AEM = OMA - AOM.
2. Найдем значение угла FAM (угол центральный):
Угол FAM равен углу FAG (центральный) плюс угел GAF (вписанный).
Значит, FAM = FAG + GAF.
Решение по шагам:
1. Найдем центральный угол AEM:
- угол OMA = 360° (из свойства центрального угла в окружности)
- AEM = OMA - AOM = 360° - 55° = 305°
2. Найдем центральный угол FAG:
- угол OMF = 360° (из свойства центрального угла в окружности)
- FAG = OMF - FOM = 360° - 110° = 250°
3. Найдем вписанный угол GAF:
- угол GAF = угол центральный FAG/2 = 250°/2 = 125°
4. Найдем угол FAM:
- FAM = FAG + GAF = 250° + 125° = 375°
Теперь ответы на вопросы:
1. Х = AEM = 305°
2. Треугольник FMA можно определить как остроугольный, поскольку сумма всех его углов (FAM, FMA, MAF) равна 180°, а угол FAM составляет 375°, что больше 180°.