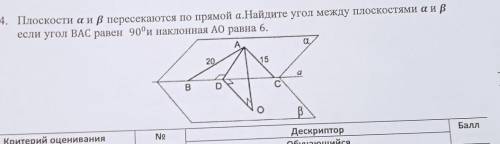
плоскости Альфа и Бета пересекаются по прямой а Найдите угол между плоскостями Альфа и Бета если угол AC равен 90 градусов а наклонная равна 6

Для решения данной задачи, нам потребуется использовать данные о трех точках: A, B и C, которые находятся на пересечении плоскостей Альфа и Бета, а также о наклонной (прямой a) и угле AC между наклонной и плоскостью Альфа.

Для начала, определим, как расположены точки A, B и C относительно друг друга на поверхностях Альфа и Бета:
- Точка A является общей для обеих плоскостей, так как плоскости пересекаются по прямой a.
- Точка C лежит на плоскости Альфа и образует прямой угол (90 градусов) с наклонной a.
- Точка B находится на плоскости Бета, но позиция этой точки точно не определена в задаче.

Теперь мы можем приступить к построению решения. Для этого воспользуемся следующими шагами:

Шаг 1: Найдем векторы, лежащие на плоскостях Альфа и Бета.
Вектор нормали (перпендикуляра) к плоскости Альфа можно найти, используя векторное произведение двух векторов, лежащих на плоскости. Обозначим эти векторы как v1 и v2:
v1 = AB
v2 = AC
Заметим, что плоскость Альфа проходит через точки A и C. Поэтому, вектор, лежащий в плоскости Альфа, можно получить, вычтя друг из друга эти два вектора: v1 - v2.

Вектор нормали к плоскости Бета можно найти аналогичным образом, используя другие два вектора: v2 и v3.
v3 = BC

Шаг 2: Найдем угол между векторами нормалей.
Угол между двумя векторами можно найти, используя следующую формулу:
cos(θ) = (v1 • v2) / (|v1| * |v2|)
где • обозначает скалярное произведение векторов, и | | обозначает модуль (длину) вектора.

Чтобы найти угол θ, принимаем во внимание, что векторы нормалей -- это векторы, лежащие на плоскостях. Поэтому, их длины равны:
|v1| = |v2| = |v3| = 1 (если плоскость вертикальная)

Шаг 3: Вычисляем угол между плоскостями.
θ = arccos(cos(θ))

Итак, для решения этой задачи, мы должны найти два вектора нормалей (v1 и v2), вычислить угол между ними, а затем найти угол между плоскостями, используя полученное значение угла.

Приступим к решению. Пусть A(1,2,3), B(x,y,z), C(4,6,7).

Шаг 1: Находим векторы нормалей.
v1 = AB = (x-1, y-2, z-3)
v2 = AC = (4-1, 6-2, 7-3) = (3, 4, 4)
Вектор нормали плоскости Альфа: n1 = v1 - v2 = (x-1, y-2, z-3) - (3, 4, 4) = (x-4, y-6, z-7)
Аналогично, вектор нормали плоскости Бета: n2 = v2 - v3 = (3, 4, 4) - (x-4, y-6, z-7) = (7-x, 6-y, z-1)

Шаг 2: Находим угол между векторами нормалей.
cos(θ) = (n1 • n2) / (|n1| * |n2|)
Подставляем значения векторов нормалей и модулей:
cos(θ) = ((x-4)(7-x) + (y-6)(6-y) + (z-7)(z-1)) / (sqrt((x-4)^2 + (y-6)^2 + (z-7)^2) * sqrt((7-x)^2 + (6-y)^2 + (z-1)^2))

Шаг 3: Вычисляем угол между плоскостями.
θ = arccos(cos(θ))

Теперь, если мы подставим значения координат B(x,y,z) в формулу, мы сможем найти угол между плоскостями Альфа и Бета.

Однако, в данной задаче не даны значения координат точки B, поэтому невозможно рассчитать точное значение угла между плоскостями. Для полного решения нужны данные о точке B.

Данный подход является общим и может быть использован для решения задач, подобных этой. Важно понимать, что для точного решения необходимо иметь полное множество данных, включая значения координат точки B.