Плоскость, пересекающая ось цилиндра, пересекает основания цилиндра по хордам, длины которых равны 6 и 8. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра, если диаметр основания равен 10, а образующая 14.
Другие вопросы по теме Геометрия
Популярные вопросы
- Составьте уравнения реакции: а) углерод + металл(1) б) углерод + металл(2)...
1 - Начертите координатную прямую и отметьте на ней точки с координатами: М(1),...
3 - Составьте предложения с данными словами, где бы они выступали рас обособленными...
2 - Под быстротой как физическим качеством человека понимается: а) скорость перемещения...
3 - 1) Как звали хана золотой Орды, который воспользовался этим и двинулся на Москву...
2 - Диагональ BD прямоугольника ABCD со стороной BC образует угол в 30°. Вычисли...
2 - Укажите представители каких партий являются членами госдумы рф...
1 - Составить из слов go to the like go to the seaside go to the mountains по одному...
2 - Английский язык нужно заранеее...
3 - Знайдіть суму перших десяти членів арифметичної прогресії,якщо А1=4,А10=-10...
3
Объяснение:
Плоскость, пересекающая ось цилиндра, пересекает основания цилиндра по хордам, длины которых равны 6 и 8. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра, если диаметр основания равен 10, а образующая 14.
Объяснение:
Радиус 10:2=5. Т.к. образующая 14, то ОО₁=14 .
Пусть ОМ=х, тогда МО₁ =14-х.
1) а)Пусть ОС⊥АВ. Тогда ОС в равнобедренном ΔАОВ, является медианой и АС=1/2АВ=1/2*6=3
В ΔАСО-прямоугольном , по т. Пифагора СО=√(5²-3²)=4
б)Пусть О₁С₁⊥А₁В₁. Тогда О₁₁С в равнобедренном ΔА₁О₁В₁ , является медианой и А₁С₁=1/2А₁В₁=1/2*8=4
В ΔА₁С₁О₁-прямоугольном , по т. Пифагора С₁О₁=√(5²-4²)=3.
2) Т.к. основания цилиндра параллельны, то ΔСОМ∼ ΔС₁О₁М по 2-м углам(∠СМО=∠С₁МО₁ как вертикальные, ∠СОМ=∠С₁О₁ М как соответственные) ⇒ сходственные стороны пропорциональны,
3) Линейным углом между плоскостью сечения и основанием будет ∠МС₁О₁ :
т.к. если проекция С₁О₁ ⊥А₁В₁ , то и наклонная МС₁⊥А₁В₁ .
ΔМО₁С₁ -прямоугольный, tg∠МС₁О₁ =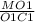 =
=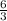 ⇒ tg∠МС₁О₁=2.
⇒ tg∠МС₁О₁=2.