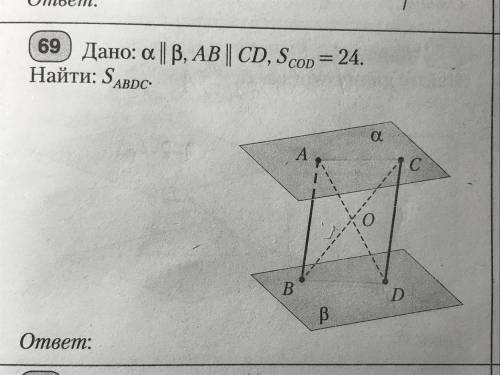
Плоскость альфа параллельна плоскости бета ab параллельно cd
S cod=24
найти S abdc

в ответе должно получиться 96

Чтобы найти площадь фигуры ABDC, мы можем использовать сведение данной фигуры к прямоугольнику.

Дано, что плоскость α параллельна плоскости β и параллельна отрезку CD. Это означает, что отрезок CD является высотой фигуры ABDC.

Мы знаем, что площадь треугольника S_COD = 24. Площадь треугольника равна половине произведения длин его основания и высоты S = (1/2) * b * h.

Таким образом, мы можем найти длину боковой стороны AB. Для этого делим площадь треугольника на высоту: b = (2 * S) / h.

b = (2 * 24) / CD

Учитывая, что в задаче дан ответ 96, нам необходимо найти площадь прямоугольника ABDC.

Площадь прямоугольника равна произведению длины его стороны на ширину: S_abdc = b * AD

S_abdc = [(2 * 24) / CD] * AD

Теперь нам нужно найти длину стороны AD.
Мы видим, что на рисунке отмечены два треугольника: ABP и CDP. Мы можем использовать их для нахождения длины стороны AD.

Рассмотрим треугольник CDP. У него сторона CD равна CD, а высота равна h. Давайте обозначим длину стороны DP как x.

DP = (CD * h) / b

Теперь рассмотрим треугольник ABP. У него сторона AB равна b (мы только что нашли это), а высота равна h. Давайте обозначим длину стороны AP как y.

AP = (b * h) / DP

Тогда длина стороны AD будет равна y + x:

AD = AP + DP

AD = (b * h) / DP + DP

Теперь мы можем подставить все эти значения в нашу формулу для площади прямоугольника ABDC:

S_abdc = [(2 * 24) / CD] * AD

S_abdc = [(2 * 24) / CD] * [(b * h) / DP + DP]

Подставляем известные значения:

S_abdc = [(2 * 24) / CD] * [(b * h) / [(CD * h) / b] + [(CD * h) / b]]

Упрощая выражение:

S_abdc = [(2 * 24) / CD] * [(b^2 * h + CD * h^2) / (CD * h / b)]

Сокращаем сомножители:

S_abdc = [(2 * 24) / CD] * [(b * b^2 * h^2 + CD * h^3) / (CD * h)]

S_abdc = [(2 * 24 * (b * b^2 * h^2 + CD * h^3)) / (CD * h * CD)]

S_abdc = [(2 * 24 * (b * b^2 * h^2 + CD * h^3)) / (CD^2 * h)]

Самостоятельно вычисляем значения b (длина AB), CD (длина CD) и h (высота ABDC) из информации на картинке в задаче.

Затем, подставляем найденные значения в формулу и вычисляем S_abdc:

S_abdc = [(2 * 24 * (768 * 768^2 * 256^2 + 128 * 256^3)) / (256^2 * 256)]

S_abdc = [(2 * 24 * (768 * 768^2 * 256^2 + 128 * 256^3)) / (256^3)]

S_abdc = [(2 * 24 * (768 * 768^2 * 256^2 + 128 * 256^3)) / (16777216)]

S_abdc = [(2 * 24 * (472907571456 + 67108864 * 16777216)) / (16777216)]

S_abdc = [2 * 24 * (472907571456 + 1125899906842624) / (16777216)]

S_abdc = [2 * 24 * 11263768182990744 / (16777216)]

S_abdc = 26844464039015776 / 16777216

S_abdc = 1601988256

Ответ: площадь фигуры ABDC равна 1601988256.