Плоские углы при вершине А пирамиды - прямые, АД=АВ=АС, Sполн=12+4v3. Найдите ВС

Ответы

ElizabethFoxEl 25.07.2022 20:40

ответ.

Треугольная пирамида , все её грани равны , так как все грани -

прямоугольные треугольники с равными катетами : AD=AB=AC ,

∠СAD=∠BAD=∠САВ=90° .

Обозначим катеты через а . Тогда площадь одной грани равна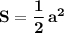 $\bf S=\dfrac{1}{2}\, a^2$ . А площадь полной поверхности равна сумме площадей

трёх одинаковых граней , то есть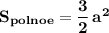 $\bf S_{polnoe}=\dfrac{3}{2}\, a^2$ .

Найдём квадрат катета:

$\dfrac{3}{2}\, a^2=12+4\sqrt3\ \ \ \Rightarrow \ \ \ a^2=\dfrac{2\cdot (12+4\sqrt3)}{3}=\bf \dfrac{8\cdot (3+\sqrt3)}{3}$

Найти надо ВС - гипотенузу прямоугольного треугольника с катетами, равными а . По теореме Пифагора имеем

$BC^2=AC^2+AB^2=a^2+a^2=2a^2=\dfrac{16\cdot (3+\sqrt3)}{3}\ ,boldsymbol{BC}=\sqrt{\dfrac{16\cdot (3+\sqrt3)}{3}}=4\cdot \sqrt{\dfrac{3+\sqrt3}{3}}=\bf 4\cdot \sqrt{1+\dfrac{\sqrt3}{3}}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

hplss 18.07.2019 07:50

Внешний угол треугольника при вершине b в три раза больше его внутреннего угла a и на 40 градусов больше внутреннего угла c.найдите углы треугольника. !...

MaveJ 18.07.2019 07:50

Даны две пересекающиеся прямые ав и сд в точке о угол аод равен 53 градусов . найти остальные углы...

NoNameKek1Himka 18.07.2019 07:50

Найдите площадь прямоугольника если отношения соседних сторон равно 5: 7 а периметр равен 48...

Аиляра 18.07.2019 07:50

Решить ! ! треугольника авс равнобедренный. угол авс равен 20 градусов. через вершину в данного треугольника проведена прямая еf, параллельная прямой ас. найдите: 1) угол аве;...

likagluxova 03.05.2021 07:47

Геометрия . №1 Точка С – середина отрезка АВ. Найдите координаты точки В, если А (5;-3), С (-1;2). Не пишите спам, уважительная . Сразу буду жалобы на спам кидать....

rahbfwBbdqbqdI 03.05.2021 07:52

Геометрия . №2 а)АВ – диаметр окружности с центром О. Найдите координаты центра окружности, если А (-5;4) и В(7;2). b) ( ) Запишите уравнение окружности, используя условия пункта...

nikipana 03.05.2021 08:01

Решите задачи устно и запишите только ответы...

sashka2006123 22.09.2019 11:20

Вправильной четырёхугольной пирамиде все рёбра равны 1. через сторону основания и среднюю линию противолежащей боковой грани проведена плоскость. а)докажите, что сечением пирамиды...

hhhf1fodjcnj 22.09.2019 11:20

Окружность с центром o касается прямой ab в точке m. угол mbo равен 21 градусу. чему равны остальные углы mbo...

лидусик13 22.09.2019 11:20

Кут при вершин ривнобедриного трикутника = 40°. знайти кут при основі...

Плоские углы при вершине А пирамиды - прямые, АД=АВ=АС, Sполн=12+4v3. Найдите ВС

Популярные вопросы