Площаль из прямоугольного треугольника равна 98√3 один из острых углов равен 60°найдите длинну катета прилежащегок этому углу
Другие вопросы по теме Геометрия
Популярные вопросы
- составить 6 предложений По содержанию предложения Аля в Стране...
3 - Собрать информацию о природных ресурсах Казахстана. Использование...
2 - Розв яжи рівняння 5,8:5=х:4,75...
1 - Выпишите номера правильных суждений: А) Корневую систему, в...
2 - CИЛА ТРЕНИЯ Когда тело останется в состоянии покоя под действием...
1 - Вычислить производные функций:...
3 - Напишите сочинения на одну из тем: 1) Какими должны быть взаимоотношения...
1 - Что называется драйвером устройства? программа, осуществляющая...
2 - Написать уровнение РАСПАДА солей на ионы.а) NaNO3б) AlCIв) Na2CO3г)...
1 - 1 каких обработках звучит кюй АДАЙ ? ( народную не писать) 2...
3
ответ: 13
Пошаговое решение:
1) Если один из углов прямоугольного треугольника равен 60°, тогда его второй острый угол будет равен 30°.
2) Катет, лежащий против угла 30°, равен половине гипотенузы, т.к. синус угла 30° = 0.5, а в прямоугольном треугольнике синус угла - это отношение противолежащего ему катета к гипотенузе.
3) Катет, лежащий против угла 60°, равен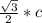 , где
, где  - гипотенуза.
- гипотенуза.
4) Площадь прямоугольного треугольника равна полупроизведению его катетов. Отсюда: . Получаем уравнение:
. Получаем уравнение:
Так как катет, прилежащий к углу 60°, равен половине гипотенузы ( ), то он равен 13.
), то он равен 13.