1. Геометрия
  2. Площадь прямоугольника

Площадь прямоугольника равна 49√3 см², а угол между его диагоналями - 60°. найти стороны

letochka111 letochka111    2   01.10.2019 10:50    13

Ответы
Artur2021 Artur2021  27.08.2020 10:49

Формула площади параллелограмма: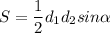 S = \dfrac{1}{2}d_1d_2sin\alpha, так как прямоугольник - частный случай параллелограмма и его диагонали равны, то формула перепишется так: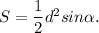 S = \dfrac{1}{2}d^2sin\alpha.

Из площади найдём диагональ прямоугольника: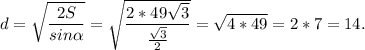 d = \sqrt{\dfrac{2S}{sin\alpha}} = \sqrt{\dfrac{2*49\sqrt3}{\frac{\sqrt3}{2}}} = \sqrt{4*49} = 2*7 = 14. (см).

Рассмотрим треугольник, образованный двумя половинками диагоналей и одной из сторон треугольника (выделен зелёным на рисунке). Так как мы имеем дело с прямоугольником, половинки диагоналей равны, значит треугольник равнобедренный. Так как угол между диагоналями равен 60°, то данный треугольник - равносторонний, ведь все углы равностороннего треугольника по 60°.

Значит ширина прямоугольника равна половине диагонали, то есть: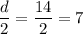 \dfrac{d}{2} = \dfrac{14}{2} = 7 (см).

Длину найдём по теореме Пифагора из треугольника образованного диагональю и двумя смежными сторонами прямоугольника: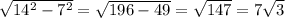 \sqrt{14^2 - 7^2} = \sqrt{196 - 49} = \sqrt{147} = 7\sqrt{3} (см).

Так же длину можно было найти из площади: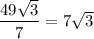 \dfrac{49\sqrt3}{7} = 7\sqrt3 (см).

ответ: длина 7√3 см, ширина 7 см.
Площадь прямоугольника равна 49√3 см², а угол между его диагоналями - 60°. найти стороны
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
tadzhigul tadzhigul  04.05.2020 14:21
Знайти катет прямокутного трикутника протенція якого на гіпотенузи дорівнює 5 см а гіпотенузи 9,8...
lbogdan2 lbogdan2  04.05.2020 14:21
До ть розв язати, геометрія 11 клас ів...
Тжвик Тжвик  04.05.2020 14:20
2. У прямокутному трикутнику АВС( А = 900) ВС=4см, В =β. Знайдіть АВ....
Zhenkyaaaa Zhenkyaaaa  04.05.2020 14:21
Що є геометричним місцем точок рівновіддалених від сторін кута AOB (кут AOB дорівнює 180°)...
perrezz perrezz  04.05.2020 14:21
Основа прямої призми є ромб зі стороною 5 см і однією з діагоналей 8 см,бічне ребро 13 см. Знайти об єм призми​...
qooperty qooperty  04.05.2020 14:21
Сколько м2 ткани потребуется для пошива шатра цирка «Шапито», если диаметр шатра составляет 32 м, а высота 22 м, причем высота крыши равна 12 м? (Добавить 5% ткани...
кузя216 кузя216  10.09.2020 18:16
с решением желательно с чартежем...
PORCH1488 PORCH1488  10.09.2020 18:55
Задача: 1. Побудуйте прямі і , що перетинаються в точці 2. Побудуйте прямі і , що перетинаються в точці і перетинають прямі і відповідно в точках С, D і M, N 3....
mishac1470 mishac1470  11.09.2020 18:16
найти точки что лежат на......
Русланн2521 Русланн2521  10.09.2020 18:59
Якщо при перетині двох прямих січною сума внутрішніх односторонніх кутів не дорівнює 180 ˚ , то відповідні кути…​...

Популярные вопросы