Площадь боковой поверхности конуса равна 60пи см^2. расстояние от центра основания до образующей равна 4,8 см. найти объем конуса.

Ответы

anonim869 02.10.2020 17:04

Дано : конус, OC = OA = R, BA = BC =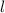 - образующие,

Sбок = 60π см² , OD⊥BC, OD = 4,8 см

Найти : V

BO = h - высота конуса, ΔВОС - прямоугольный

ΔВОС ~ ΔВDО по общему острому углу ∠OBD

$\dfrac {BC}{BO}=\dfrac{OC}{OD}\ \ \Rightarrow\ \ OC\cdot BO=OD\cdot BC\ \ \Rightarrow\ \ \boldsymbol{Rh=4,8l}$

Sбок = $\pi Rl=60\pi\ \ \ \Rightarrow\ \ \ \boldsymbol{R=\dfrac{60}l}$

Объём конуса

$V=\dfrac 13\cdot \pi R^2h=\dfrac {\pi}3\cdot R\cdot Rh=\dfrac {\pi}3\cdot \dfrac{60}l\cdot 4,8l=\pi\cdot 20\cdot 4,8=96\pi$

ответ : 96π см³

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

keramix 09.09.2019 21:16

ОксанаБ80 09.09.2019 21:16

Gfdsahjk 09.09.2019 21:16

НИкитос1757 09.09.2019 21:17

angeldeikina 09.09.2019 21:17

Ярешил, (просто нужно проверить) ...

khsush 09.09.2019 21:19

Лизунчик011 09.09.2019 22:20

varvaralikhtsr 09.09.2019 21:20

dogdogdogdogdogdog 09.09.2019 21:20

lizarodionov6Liza 09.09.2019 21:20