Площадь боковой грани правильной треугольной пирамиды составляет площади основания. найдите высоту пирамиды, если сторона основания равна 2.

Ответы

bonbino1 17.06.2020 08:16

Основание - правильный треугольник со стороной 2.

Тогда высота этого треугольника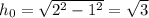 $h_{0} = \sqrt{2^2-1^2}=\sqrt{3}$

Высота пирамиды делит высоты треугольника в соотношении 1:2, т.е.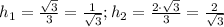 $h_{1}=\frac{\sqrt{3}}{3}=\frac{1}{\sqrt{3}}; h_{2}=\frac{2\cdot\sqrt{3}}{3}=\frac{2}{\sqrt{3}}$

Площадь боковой грани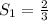 $S_{1}=\frac{2}{3}$ , основание - 2 => высота боковой грани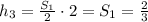 $h_{3} = \frac{S_{1}}{2}\cdot 2 = S_{1} = \frac{2}{3}$

Т.о. высота пирамиды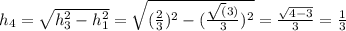 $h_{4} = \sqrt{h_{3}^2 - h_{1}^2} = \sqrt{(\frac{2}{3})^2-(\frac{\sqrt(3)}{3})^2}=\frac{\sqrt{4-3}}{3}=\frac{1}{3}$

ответ: $\frac{1}{3}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

kozlov20041 19.11.2020 09:21

- Эгерде:1) a=9, b=11, y=70°; 2) а=3, с=5, B=130°18 ; 3) b=1,4, c=2,5, а=35°34 болсо, АВС үч бурчтугунун белгисиз жагынтапкыла....

nastialeon 22.12.2020 07:58

4. Равные между собой отрезки МК и PN составляютравные углы с отрезком KN. Докажите, что NM-КР....

Viktoria070804 22.12.2020 07:58

Есть ответы сочч на казахском Соч по геометрии ...

Полина89750 22.12.2020 07:58

Стороны треугольника ABC равны BC = 15 см, AB = 13 см, AC = 4 см соответственно. Плоскость α проведена через стенку ЛК. Найти размер угла между плоскостью α и треугольником,...

гтто5 22.12.2020 07:59

Прямая, параллельная стороне АС треугольника АВС пересекает стороны АВ и ВС в точках М и N соответственно. Найти NC, если АС=111, MN=37, BN=30....

vityabro13 22.12.2020 07:59

2. При каких значениях х и у точки А (3;у) и В (х; 5) симметричны относительно начала координат?А) х = — 3, y = 5 В) х = 3, y = 5 С) х = 5, у = -3 D) x=5. у = 3...

eviilevii123 22.12.2020 08:00

У выражение 1син² а/кос²- син²а...

Лесолес 22.12.2020 08:00

Найти расстояние Ав б) средину отрезка Ав А(-4;1;-6),В(-3;3;-4)...

fomax1337 25.05.2019 06:50

Как понять равнобедренный треугольник...

LeraLis201 25.05.2019 06:50

Даны прямые а и б.если а параллельно б,то параллельно ли б а?...

Площадь боковой грани правильной треугольной пирамиды составляет площади основания. найдите высоту пирамиды, если сторона основания равна 2.

Популярные вопросы