Первая прямая проходит через точки A=(-13;-6) и B=(-5;-8). Вторая прямая проходит через точки C=(11;-2) и D=(18;-4). Найдите координаты точки пересечения этих прямых. ответ запишите в виде "(12;-34)". Без пробелов и через точку с запятой
Другие вопросы по теме Геометрия
Популярные вопросы
- С какого класса изучают алгебру ...
3 - «Ай мен Күн» ертегісін (20. mp3) тындап, мазмұн, стиль жағынан оқылым мәтінінен...
1 - Choose the correct word 1 I don t want anything/anybody to eat, thanks. 2 Suzie...
1 - Складіть і запишіть висловлення (5-8 речень) у науковому стилі на тему, яку...
3 - 6 Ask and answer questions.1 l/take pictures?A: Can I take pictures here?B:...
3 - почему высказывание п. тосканелли о достижении стран на другой стороне земного...
2 - B = 11; b на 35 л193. На первом тракторе работали 60 ч,60 ч, на втором55 ч....
1 - Чому набір висотних поясів неоднаковий на західних і східних схилах Кордилєр...
1 - выпиши выделенные глаголы с существительными (определить форму имени существительного...
2 - Обчисліть яка маса сульфур (VI) оксиду вступить в реакцію з водою, якщо при...
2
(-82; 291)
Объяснение:
Пусть прямая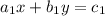 проходит через точки
проходит через точки 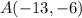 и
и 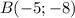 , тогда имеем систему уравнений:
, тогда имеем систему уравнений:
Аналогично прямой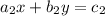 предположим, что она проходит через точки
предположим, что она проходит через точки 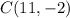 и
и 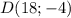 , составим систему:
, составим систему:
Для того чтобы найти точку пресечения прямых составляем систему
Таким образом имеем точку пересечения (-82; 291)