1. Геометрия
  2. Первая прямая проходит

Первая прямая проходит через точки А=(11;-5) и В-(4;-6). Вторая прямая проходит через точки С= (-22;-4) и D=(-28;-5). Найдите координаты точки пересечения этих прямых. ответ запишите в виде "(12;-34)". Без пробелов и через точку с запятой.

maxshcherba5p08v6b maxshcherba5p08v6b    1   03.12.2021 23:40    19

Ответы
VERONIKA114561378 VERONIKA114561378  18.01.2022 18:41

(26;4)

Объяснение:

Так как наши графики являются прямыми, функции выглядят так: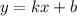 y=kx+b

Найдем значения k и b, подставив значения точек A и B в уравнение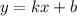 y=kx+b и решив следующую систему:

\left \{ {{-5=11k+b} \atop {-6=4k+b}} \right.

\left \{ {{k=\frac{b+5}{11} } \atop {b=-6-4k}} \right.\\\\k=\frac{-6-4k+5}{11} | * 11\\11k = -6-4k+5\\15k=-1\\k=-\frac{1}{15}

Найдем b, подставив в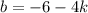 b=-6-4k:

b=-6+\frac{4}{15} =-\frac{90}{15}+\frac{4}{15} =\frac{86}{15}

Первое уравнение имеет такой вид: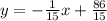 y=-\frac{1}{15}x+\frac{86}{15}

- - - - - -

Найдем второе уравнение по аналогии (мне лень расписывать системами, так что я буду писать просто через новую строчку и в конце запишу итоговое решение системы)

\left \{ {{-4=-22k+b} \atop {-5=-28k+b}} \right.

- - - - -

22k=4+b\\k=\frac{4+b}{22}\\

b=-5+28k \\k=\frac{4-5+28k}{22} \\k=\frac{28k-1}{22} | * 22\\22k=28k-1\\-6k=-1\\k=\frac{1}{6}

- - - - -

b=-5+\frac{28}{6} = -\frac{30}{6} + \frac{28}{6} =-\frac{2}{6}

\left \{ {{k=\frac{1}{6} } \atop {b=-\frac{2}{6} }} \right.

Второе уравнение имеет следующий вид: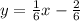 y=\frac{1}{6}x-\frac{2}{6}

Чтобы найти точку пересечения, нужно приравнять уравнения графиков.

-\frac{1}{15} x + \frac{86}{15} = \frac{1}{6} x-\frac{2}{6} | * 30\\-2x+172=5x-10\\-7x=-182\\x=26\\

Чтобы найти y, нужно подставить в любое уравнение значение x.

y=\frac{26}{6} -\frac{2}{6} =\frac{24}{6} =4

ответ: (26;4)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
kristka98 kristka98  28.02.2019 22:30
Периметр прямоугольника равен 22 дм. найдите сумму длин расстояний от любой внутренней точки прямоугольника до его сторон...
ХлойкаПрайс ХлойкаПрайс  28.02.2019 22:30
.(Один из углов прямоугольной трапеции равен120*,большая боковая сторона=20 см, а средняя линия =7см. найдите основания трапеции)....
лалвллв лалвллв  28.02.2019 22:30
.(Точка e и f лежат соответственно на сторонах ad и bc параллелограмма abcd ,причём ae=ed, bf: fc=4: 3)а)выразите вектор еf через векторы m=ab и n=ad ) б )может ли...
жсдрю жсдрю  28.02.2019 22:30
Как построить параллелограмм по двум диагоналям и углу между ними...
almas05 almas05  28.02.2019 22:30
)) из точки а, лежащей вне окружности с центром в точке о, проведены две касательные. найти угол между ними, если угол между радиусами этой окружности, проведёнными...
ааааннннгггшим ааааннннгггшим  28.02.2019 22:30
.(Стороны параллелограмма равны 10 см и 3 см. биссектрисы двух углов, прилежащих к большей стороне делят противоположную сторону на три отрезка. найдите эти отрезки)....
домкорытосыгуьдатсс домкорытосыгуьдатсс  28.02.2019 22:20
Найдите точки пересечения графика функции с осью абсцисс: f: r, f (x)=3-x (черта дроби) 4...
danyabro1 danyabro1  28.02.2019 22:20
Диагональ квадрата равняется 4 см. его сторона равняется диагонали второго квадрата. найдите стороны второго квадрат....
Крутой649 Крутой649  28.02.2019 22:20
.(Высота ромба, которая проведена из вершины тупого угла, делит сторону ромба пополам. найдите периметр ромба, если длина меньшей диагонали 20 дм.)....
MadPrinter MadPrinter  07.06.2019 13:00
Вправильной четырехугольной пирамиде sabcd все ребра равны 1. найдите расстояние между прямыми as и dc....

Популярные вопросы