Периметр прямоугольника равен 22, а площадь равна 10,5. найдите диагональ этого прямоугольника.

(2x+2y =22

(x^2+y^2=10.5^2

(x+y=11

(x^2+y^2=110.25

отв :20

Объяснение:

Периметр прямоугольника определяеся по формуле

, где   a,b - стороны прямоугольника .

Если Р = 22ед., то сумма двух  соседних сторон сторон равна полупериметру, то есть 11 ед.

Пусть одна сторона прямоугольника будетx  ед. Тогда (11- x ) ед.- другая сторона . Площадь прямоугольника определяется по формуле

, a и b  стороны. Составим и решим уравнение:

Если одна сторона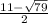 ед , то другая 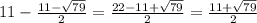ед.

Если одна сторона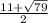 ед, то другая 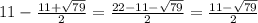ед.

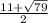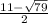Значит стороны прямоугольника  ед. и ед.

Диагональ прямоугольника найдем по теореме Пифагора : квадрат гипотенузы равен сумме квадратов катетов .

d= 10 ед.

Периметр прямоугольника:

Р = 2 * (а + b) = 22  ⇒  a + b = 11

Площадь прямоугольника:

S = a * b = 10,5

Рассмотрим закрашенный прямоугольный треугольник:

По теореме Пифагора   a² + b² = c²

Воспользуемся формулой квадрата суммы двух переменных:

(a + b)² = a² + 2*a*b + b²

11² = a² + 2*10,5 + b²

121 = a² + 21 + b²

a² + b² = 100

c² = 100   ⇒   c = ± 10  ⇒  c = 10 е.д. - диагональ прямоугольника

ответ: 10.