1. Геометрия
  2. Периметр правильного треугольника

Периметр правильного треугольника равен 2√2. Найдите площадь.

shaimyr24 shaimyr24    3   04.02.2022 03:33    43

Ответы
Taylis69 Taylis69  04.02.2022 06:00
ответ:
S=2√3/9см²

Решение:
Р=3а, где а-сторона треугольника.
а=Р/3=2√2/3ед.

S=a²√3/4=(2√2/3)²√3/4=8√3/9*1/4=
=2√3/9 см²
ПОКАЗАТЬ ОТВЕТЫ
yellowumbrella yellowumbrella  04.02.2022 06:00

У правильного (равностороннего) треугольника все стороны равны . Формула нахождения периметра правильного треугольника :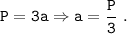 \tt P=3a\Rightarrow a=\dfrac{P}{3} ~. Итак , мы вывели формулу для нахождения стороны равностороннего треугольника . Р - это периметр (сумма длин всех сторон) ; а - сторона треугольника . Подставим наши данные : 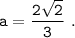\tt a=\dfrac{2\sqrt{2} }{3}~. Тогда , найдем площадь правильного треугольника по формуле : 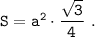\tt S=a^2\cdot\dfrac{\sqrt{3} }{4} ~. . Подставим наши данные :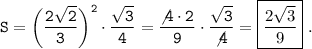 \tt S=\bigg(\dfrac{2\sqrt{2} }{3} \bigg)^2\cdot\dfrac{\sqrt{3} }{4} =\dfrac{\not4\cdot2}{9} \cdot\dfrac{\sqrt{3} }{\not4} =\boxed{\dfrac{2\sqrt{3} }{9} }~.

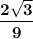ответ : \bf\dfrac{2\sqrt{3} }{9}ед.².

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
arkatovazara arkatovazara  09.04.2020 10:20
Найди радиус окружности в треугольнике ABC, угол А=90°, АВ=5 см, ВС=13 см. Найдите радиус окружности с центром С, если она имеет с прямой АВ только одну общую точку....
Полинаhelpme1 Полинаhelpme1  09.04.2020 10:20
Кожне ребро тетраедра дорівнює а. Знайдіть площу його поверхні....
vfvf2304 vfvf2304  09.04.2020 10:20
Высота правильной четырехугольной пирамиды равна 5 см а сторона основания 6 см Найдите длину бокового ребра высота правильной четырехугольной пирамиды равна 5 см а сторона основания...
l3bv1t l3bv1t  09.04.2020 10:20
На рисунке изображена окружность с центром в точке О. диаметр окружности РК=8. определите расстояние от точки А, лежащей на окружности, до точки О​...
annashevelina annashevelina  09.04.2020 10:20
с задачей, я ничего там не понял!(Если получится,то объясните как решали)...
uliatuchakrom9 uliatuchakrom9  10.03.2021 20:07
Вектор a{-3;4} вектор b{m;-9}. При каком m вектора а) коллинеарны б) перпендикулярны?...
zooz7654Кристина zooz7654Кристина  10.03.2021 20:07
У трикутнику АВС кут С=90 градусів...
петрович16 петрович16  10.03.2021 20:07
В треугольнике ABC угол C=90° AB=18° Найдите AC. ​...
aasssddddddd aasssddddddd  08.09.2019 21:00
Два угла ромба относятся как 1: 2 определите периметр ромба если его меньшая диагональ равна 12 см...
vitya48 vitya48  08.09.2019 21:00
1) периметр параллелограмма 50см.одна из его сторон на 5 см больше другой.найдите длины сторон параллелограмма. 2)в выпуклом четырёхугольнике авсд ав=сд, угол в = 70 градусов,...

Популярные вопросы