Периметр паралелограма АВCD дорівнює 10 см. Бісектриси кутів А і D перетинаються в точці М, що сторона ВС ділить відрізок АМ навпіл. Знайдіть довжини сторін паралелограма.
Другие вопросы по теме Геометрия
Популярные вопросы
- Белочка за 2ч грызет n орешков. сколько орешков она сгрызет...
2 - Определи склонение данных существительных и запиши их три столбика....
3 - Найдите значение выражения 15*(1/5)в квадрате-8*1/5...
3 - Написать уравнение гармонического колебательного движения с...
2 - Если самолёт летит со скоростью 950 км/ч,то сможет ли он за...
2 - Соседние формы рельефа гималаев.в 2-3 предложениях .!...
2 - Винни-пух сочинил за 3ч x шумелок. сколько времени ему потребуется,...
3 - Напишите транскрипции слов: мягко, вьётся, лесная....
2 - Нарисовать два отрезка в прямоугольнике, чтобы получилось восемь...
1 - Задай вопрос к предложениям начиная со слов в скобках. my father...
1
1, 1, 4, 4
Объяснение:
Сумма смежных углов параллелограмма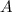 и
и 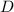 равна
равна 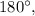 тогда
тогда 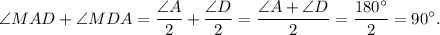
Значит треугольник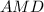 — прямоугольный,
— прямоугольный, 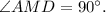
Т. к. точка — середина стороны
— середина стороны  и
и 
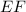 — средняя линия этого треугольника,
— средняя линия этого треугольника, 
Кроме того, как накрест лежащие, значит треугольник
как накрест лежащие, значит треугольник  равнобедренный,
равнобедренный, 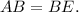
Аналогично равнобедренный и треугольник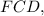
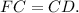
Тогда периметр