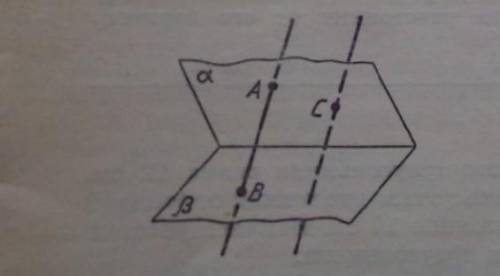
параллельные прямые ab и cd пересекаются две пересекающиеся прямые альфа и бета в четырех точках. постройте точку d по трем заданным точкам a b и c​

Для решения данной задачи, нам необходимо следовать определенному алгоритму:

Шаг 1: Вспомним основные свойства параллельных и перпендикулярных прямых.
- Параллельные прямые не пересекаются никогда. В данной задаче, это прямые ab и cd.
- Перпендикулярные прямые пересекаются и образуют прямой угол. В данной задаче, это прямые альфа и бета.

Шаг 2: По условию задачи, нам даны три точки a, b и c. Нам нужно построить точку d.

Шаг 3: Рассмотрим прямую ab. Она параллельна прямой cd. Значит, отрезок ab имеет такое же направление как и отрезок cd.

Шаг 4: Найдем прямую, которая проходит через точку c и параллельна прямой ab. Для этого проведем линию, параллельную ab, из точки c. Обозначим эту линию как прямую cd'.

Шаг 5: Поскольку прямые cd и cd' параллельны и имеют общую точку c, они являются одной и той же прямой. То есть, точка d и точка d' совпадают.

Шаг 6: Следовательно, мы можем построить точку d, проведя линию cd' через точку b.

Шаг 7: Теперь мы найдем точку пересечения прямой альфа и прямой бета. Обозначим ее точкой P.

Шаг 8: Проведем прямую через точку d и точку P. Обозначим ее как прямую dd'.

Шаг 9: Прямая dd' пересекает прямую альфа в точке d''.

Шаг 10: Точка d'' является искомой точкой д.

Таким образом, мы нашли искомую точку d, используя данные точки a, b и c, а также свойства параллельных и перпендикулярных прямых.