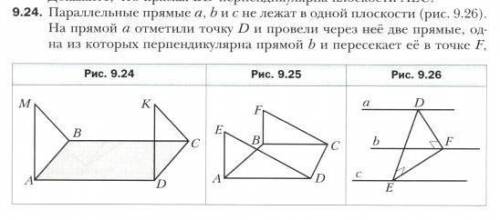
Параллельные прямые a, b и c не лежат в одной плоскости. На прямой a отметили точку D и провели через неё две прямые, одна из которых перпендикулярна прямой b и пересекает её в точке F, а другая перпендикулярна прямой c и пересекает её в точке F. Докажите, что EF ⊥ b и EF ⊥ c.
Другие вопросы по теме Геометрия
Популярные вопросы
- Замените словочитание фразеологизмамими. , мало, много, медленно, быстро....
1 - Каковы господствущие ветра (по сезонам ) африки...
2 - Расположи числа в порядке возрастания: -2; 4,7; -1,32; 0,01...
1 - 3предложения с деепричастным оборотом из обломова,...
2 - Напишите все образы героев из рассказа капитанская дочь кратко !...
2 - 25 ! надо сделать синтаксический разбор предложение. в нём можно почувствовать...
1 - Сочинить страшилку. к примеру: раз,два школа ждёт тебя три, четыре...
3 - Решите уравнение (26+33+х)+(44-13-18)-16-18-26=51...
3 - От казани до астрахани пароход идёт 3 дня,а обратно 4 дня. за сколько...
3 - Что такое рубинчик, скажите , нужно...
2
Для начала, давайте рассмотрим треугольник EDF. Так как EF и DF являются перпендикулярами к линиям b и c соответственно, углы EDF и FDE будут прямыми углами.
Теперь рассмотрим линии a и b. Поскольку линии a и b параллельны, угол ADB и угол FEB будут соответствующими углами и поэтому они будут равными.
Теперь рассмотрим линии a и c. Поскольку линии a и c параллельны, угол ADB и угол DEC будут соответствующими углами и поэтому они будут равными.
Теперь разделим наше рассуждение на два случая:
1. Предположим, что углы FEB и DEC не равны. Если это так, то в треугольнике EFC два угла (углы DEC и FEB) не равны 90 градусам. Это означает, что треугольник EFC не является прямоугольным, и, следовательно, линия EF не является перпендикулярной ни к линии b, ни к линии c. В этом случае наше утверждение неверно.
2. Предположим, что углы FEB и DEC равны. В этом случае оба угла DEC и FEB равны 90 градусам. Это означает, что треугольник EFC является прямоугольным, и линия EF будет перпендикулярна как к линии b, так и к линии c. В этом случае наше утверждение верно.
Таким образом, мы доказали, что если углы FEB и DEC равны, то линия EF будет перпендикулярна и к линии b, и к линии c.