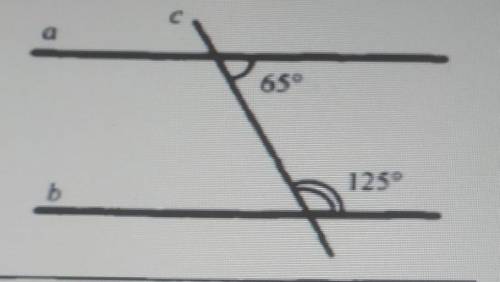
параллельны ли прямые а и б
с подробным решением

нет

Объяснение:

По теореме, если сумма односторонних углов равна 180°, то прямые, пересеченные секущей, параллельны

65°+125°=190°, получаем, что прямые а и б не параллельны

Для определения, являются ли прямые а и б параллельными, нам необходимо проанализировать их наклон или угловой коэффициент.

1) Нам даны две прямые а и б. Чтобы определить их наклон, мы должны привести их к уравнению вида y = mx + c, где m - угловой коэффициент, и c - свободный член.

Для прямой а:
Уравнение прямой а имеет вид y = -2x + 1.

Для прямой б:
Уравнение прямой б имеет вид y = -2x + 5.

2) Теперь, когда у нас есть уравнения прямых, мы можем сравнить их угловые коэффициенты. Если они равны, то прямые параллельны.

Для прямой а: угловой коэффициент м1 = -2.
Для прямой б: угловой коэффициент м2 = -2.

3) Поскольку угловые коэффициенты прямых а и б равны (-2) и совпадают, мы можем сделать вывод, что эти прямые параллельны.

В итоге, прямые а и б являются параллельными, так как их угловые коэффициенты равны и не различаются.