1. Геометрия
  2. Отрезок mh являеться диаметром.

Отрезок mh являеться диаметром. написать уравнение окружности, если м (0; 2), h (6; -2). , подробно.

propprap propprap    3   02.10.2019 04:01    32

Ответы
3мрдудец 3мрдудец  09.10.2020 10:56

Для начала, найдём координату центра окружности. Для этого воспользуемся соответствующей формулой:

О(х1+х2/2;у1+у2/2). Подставим числа и получим:

О(0+6/2;2-2/2)

О(3;0). Для того, чтобы написать уравнение окружности нам не хватает её радиуса. Найдём сначала длину диаметра, а затем выразим радиус. Теперь воспользуемся другой формулой:

d=корень из (х2-х1)^2+(у2-у1)^2. Получим:

d= корень из (6-3)^2+(-2-0)^2= корень из 13. Теперь, пришло время составить уравнение окружности. Оно будет выглядеть так:

(х-х0)^2+(у--у0)^2=r^2. Это оно в общем виде, а теперь подставим числа и получим:

(х-3)^2+у^2=13. Это и есть ответ.

ПОКАЗАТЬ ОТВЕТЫ
FenniXDouble FenniXDouble  09.10.2020 10:56
Найти уравнение окружности.

Общая формула окружности: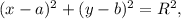 (x - a)^2 + (y - b)^2 = R^2, где (a; b) - центр окружности, R - её радиус.

Найдём координаты центра окружности.

Формула: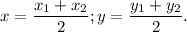 x = \dfrac{x_1 + x_2}{2}; y = \dfrac{y_1 + y_2}{2}.

\left[\begin{array}{c}x = \dfrac{6 + 0}{2} = \dfrac{6}{2} = 3,\\\\y = \dfrac{-2 + 2}{2} = \dfrac{0}{2} = 0.\end{array}

Получили точку O (3; 0).

Найдём радиус окружности.

Радиус равен расстоянию между одной из данных точек (можно выбрать любую) и центром. Можно считать расстояние по теореме Пифагора, но есть формула, которая, вообще говоря, из теоремы Пифагора и получается.

Формула: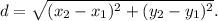 d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.

R = \sqrt{(6 - 3)^2 + (-2 - 0)^2} = \sqrt{3^2 + (-2)^2} = \sqrt{9 + 4} = \sqrt{13}.

Подставляем полученное в общую формулу окружности.

Получаем: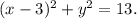 (x - 3)^2 + y^2 = 13.

ответ: (x - 3)² + y² = 13.
Отрезок mh являеться диаметром. написать уравнение окружности, если м (0; 2), h (6; -2). , подробно.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Anna69666 Anna69666  08.05.2020 18:42
кто может это все начертить на листике и прислать как фото Пусть треугольник АВС с прямым углом С. Биссектриса СК делит угол 90° пополам. Высота СН делит треугольник на два прямоугольных...
elenanatalja elenanatalja  08.05.2020 18:43
Через точку перетину двох прямих на площині проведено промінь, перпендикулярний до однієї з прямих. Знайдіть кути, утворені при перетині цих прямих, якщо даний промінь з другою...
sheealice sheealice  08.05.2020 18:43
Диаметр шара равен 5√3 см. через его конец под углом 30 к нему проведена плоскость, которая пересекает данный шар. найдите площадь сечения, полученного в результате пересечения...
viktorija0811 viktorija0811  08.05.2020 18:44
Очень В правильной треугольной пирамиде боковое ребро с плоскостью основания образует угол 45°. Высота пирамиды равна 20 см. Вычисли сторону основания пирамиды....
R5R5ty R5R5ty  08.05.2020 18:44
Площадь треугольника АВС равна S . Найдите площадь треугольника, который отсекается от треугольника АВС средней линией *S:2S:3S:4определить невозможно ОЧЕНЬ НАДО ​...
sonya0013 sonya0013  26.05.2020 16:36
Перпенжикулятом проведеный з точк M кр прямой AB ЯВЛЯЕТЬСЯ...
romakirill1999 romakirill1999  25.05.2020 16:35
Точка дотику кола вписаного у рівнобічну трапецію ділить бічну сторону на відрізки довжиною 2см і 8см. Знайдіть площу трапеції....
hzeslichestno hzeslichestno  25.05.2020 16:35
Паралелограми A1B1C1D1 і ABCD симетричні відносно деякої точки О. Знайдіть сторони паралелограмів, якщо периметр ABCD дорівнює 30 см, а В1С1=10 см....
АлинаМирнач АлинаМирнач  25.05.2020 16:35
У рівнобічній трапеції основы дорівнюють 4см і 20 см, бічна сторона 10 см. Знайдіть площу трапеції ​...
Yana7112 Yana7112  25.05.2020 16:35
В В правильной четырёхугольной призме площадь основания 144, а диагональ призмы 22. Найти объём призмы....

Популярные вопросы