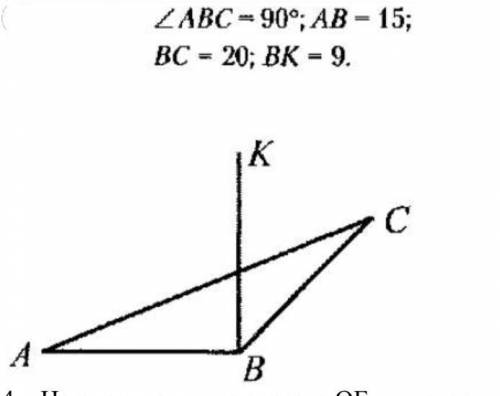
Отрезок BК перпендикулярен плоскости АВС. Найдите расстояние от точки К до прямой АС.

Чтобы найти расстояние от точки К до прямой АС, необходимо использовать понятие перпендикуляра. Поскольку отрезок ВК перпендикулярен плоскости АВС, он будет перпендикулярен и прямой АС.

Первым шагом необходимо нарисовать перпендикуляр от точки К к прямой АС. Для этого проводим перпендикулярный отрезок КМ через точку К, параллельный плоскости АВС. Также проводим отрезок КН параллельно прямой АС.

После этого, соединяем точку М и точку Н линией и получаем прямоугольный треугольник КМН.

Теперь, чтобы найти расстояние от точки К до прямой АС, необходимо найти длину отрезка КН.

Прежде всего, обратим внимание на то, что треугольник КМН прямоугольный, поскольку отрезок КМ перпендикулярен прямой АС.

Теперь воспользуемся теоремой Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы (стороны, лежащей напротив прямого угла) равен сумме квадратов длин катетов (сторон, лежащих при прямом угле).

Таким образом, расстояние от точки К до прямой АС (отрезок КН) можно найти, используя следующую формулу:

КН^2 = КМ^2 + МН^2

Теперь, зная длины отрезков, можно подставить значения в формулу и решить ее.

Полученное значение в квадрате будет представлять расстояние от точки К до прямой АС. Если необходимо найти именно расстояние, а не его квадрат, просто возьмите квадратный корень из полученного значения.

Надеюсь, что эта пошаговая инструкция поможет вам понять, как найти расстояние от точки К до прямой АС. Если у вас возникнут дополнительные вопросы, пожалуйста, не стесняйтесь задавать их.