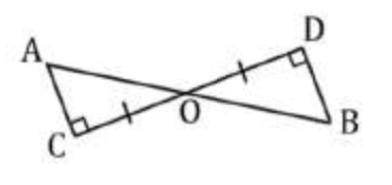
Отрезок АВ пересекает отрезок СD в его середине точке О. АС⊥СD, ВD⊥СD, СD=6,6 см, АВ=9,4 см. Найдите ВО.

Для решения данной задачи воспользуемся свойствами перпендикулярных отрезков и сходственных треугольников.

Обозначим точку пересечения отрезка АВ с отрезком СD как точку О. Также обозначим точки пересечения отрезков АС и ВD с СD как точки Е и F соответственно.

Первым шагом решения задачи будет определение длины отрезка СЕ. Поскольку СО является медианой треугольника АВС, то по свойству медианы отрезок СО делит отрезок АВ пополам. Исходя из этого, получаем:

АО = ОВ = АВ/2 = 9,4/2 = 4,7 см.

Теперь мы можем определить длину отрезка СЕ. Поскольку отрезки АС и ВЕ являются высотами прямоугольных треугольников, то они будут соответственно перпендикулярны отрезкам CD и BD. Поэтому, треугольники АСЕ и ВОD будут сходственными. Исходя из сходства треугольников, получаем:

СЕ/АС = ОD/ВD.

Так как CD = 6,6 см, а АВ = 9,4 см, то можно определить длину отрезка АС:

АС = AB - BC = 9,4 - 6,6 = 2,8 см.

С учетом этого, получаем:

СЕ/2,8 = ОD/ВD.

Теперь определим длины отрезков ОD и ВD. Так как О является серединой отрезка CD, то длина отрезка ОD будет равна половине длины CD:

ОD = CD/2 = 6,6/2 = 3,3 см.

Также, поскольку BD является высотой прямоугольного треугольника ВOD, то определим длину отрезка ВD с использованием теоремы Пифагора:

BD² = OD² + OB²,
BD² = 3,3² + 4,7²,
BD² = 10,89 + 22,09,
BD² = 33,98,
BD = √33,98 ≈ 5,83 см.

Теперь мы можем определить длину отрезка СЕ:

СЕ/2,8 = 3,3/5,83,
СЕ = (2,8 * 3,3)/5,83 ≈ 1,58 см.

Наконец, для того чтобы найти длину отрезка ВО, сложим длины отрезков ВD и ДЕ:

ВО = ВD + ДЕ = 5,83 + 1,58 = 7,41 см.

Таким образом, длина отрезка ВО равна 7,41 см.