Отрезок AD - биссектриса треугольника АВС. Найдите: 1) отрезки BD и CD, если AB = 10 см, AC = 12 см, ВС= = 11 см; 2) сторону AC, если BD: DC = 4:9, AB = 16 см; 3) стороны AB и AC, если AB + AC = 32 см, BD: DC = = 5: 3.
Другие вопросы по теме Геометрия
Популярные вопросы
- 3. Энергия электрического поля конденсатора 235Список заданий00:13:35Условие...
1 - Ребята Хто з гравців задньої лінії допустив помилку при виконанні нападаючого...
3 - Приведи к одному показателю корня 5√5 и 128√35 (к наименьшему показателю)....
1 - посоветуйте мангу -мынхву яой...
1 - Артем предложил что купол зонта имеет форму сферического сегмента. Вычислите...
2 - Имя: Гермес Какие силы природы:??? Покровителем чего считался:??? Имя: ГераКакие...
1 - Чем важна для других деятельность Правдина?...
2 - найди значение выражения не забудьте округлить, не знаю как делать это к...
3 - Все мы, увы, не ко всем делам одинаково годны». Приведи примеры из жизни...
2 - завдання ДПА неможу рішити...
3
Объяснение:
A
/|\
/ | \
/ | \
/|\
C D B
А) отрезки BD и CD, если AB = 10 см, AC = 12 см, ВС= = 11 см;
1)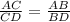 это по правилу (не помню как называлось)
это по правилу (не помню как называлось)
BC=CD+BD=11
Легче будет представить, если CD=x, BD=y
1)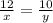
2)x+y=11
1)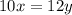
2)x=11-y
подставим
10(11-y)=12y
110-10y=12y
22y=110
y=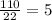
x=11-5=6
СD=6 см
BD=5 см
2)сторону AC, если BD: DC = 4:9, AB = 16 см;
тоже используем эту схему
Пусть BD=4x, DC=9x
Тогда из того правила
3) стороны AB и AC, если AB + AC = 32 см, BD: DC = = 5: 3.
Пусть AB=x, AC=y, тогда
AB=20 см
AC= 12 см