Острый угол прямоугольного треугольника равен 60°,а высота опущенная на гипотенузу равна 21. Найдите больший из катетов данного треугольника
Другие вопросы по теме Геометрия
Популярные вопросы
- Решите неравенства с соответствующих уравнений k -67 94...
3 - Нужно разделить на группы : согласование , примыкание , ...
1 - Лежащая на столе книга давит вниз с некоторой силой. стол действует на...
1 - Объем иодоводорода (при н. если йодоводород образовался взаимодействием...
1 - Решите с дискрименанта x²-6x-3=0 x²-3x+11=0...
3 - Решите номер 6 и дополнительное...
1 - Назовите бинарные соединения. kh fecl3 cucl2 na2s пример nah- гидрид натрия...
1 - Только после вас - какой разряд...
3 - Would you like to englishman? a)the/- b)an/the c)a/- d)a/an e)the/an ...
3 - Умоляю это на отметку я не шарю ответ должен быть 32 но я хз как решать....
1
42.
Объяснение:
Пусть задан треугольник с катетами a и b и гипотенузой c. Высота h = 21 опущена из вершины С на гипотенузу с, а угол А = 60°. Второй острый угол этого прямоугольного треугольника равен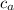 большего катета a на гипотенузу.
большего катета a на гипотенузу.
∠В = 90° - 60° = 30°. Больший катет всегда лежит против большего угла, поэтому большим катетом является катет а, лежащий против большего угла А.
Рассмотрим прямоугольный треугольник, образованный большим катетом a заданного треугольника, высотой h, опущенной на гипотенузу и проекцией
В этом треугольнике гипотенузой является больший катет a заданного треугольника, а высота h = 21 является катетом, лежащим против ∠В = 30° .
Известно, что катет, лежащий против угла в 30°, равен половине гипотенузы. Поэтому b = 2h = 2 · 21 = 42.