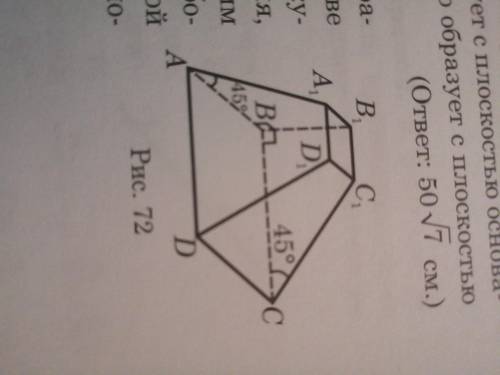
Основанием усечённой пирамиды является квадрат. Две боковые грани перпендикулярны к плоскости основания, а две другие образуют с ним угол 45 градусов. Найдите площадь боковой поверхности усечённой пирамиды, если стороны оснований а и 2а (рис. 72)
Другие вопросы по теме Геометрия
Популярные вопросы
- Выразите числа 9/37 и 1 3/28 в виде прибленого значения десятичной дроби до сотых...
3 - Моторная лодка едет 2 часа расстояние в 60 км за какую скорость в километрах в...
3 - Объем прямоугольного паралелепипеда равен 12целых 4/33 см в кубе,длина-2целых...
1 - Всостав выделительной системы земноводных входят а) кишечник б) мочеточник в)...
2 - Велосипедист в течение двух часов проехал 36 км. какова средняя скорость велосипедиста,...
2 - Составьте план по теме бородинское сражение по пунктам...
1 - Какую роль в жизнедеятельности животных играет симметрия их тела...
2 - Что объединяет имена феофан грек андрей рублев дионисий?...
1 - На тело, погруженное в керосин, действует архимедова сила 4н. какая архимедова...
1 - Слова с окончаниями ие ия ий в косвенных падежах сущевствительные...
1
1. Начнем с прямоугольника. В данном случае, это боковая грань, которая перпендикулярна к плоскости основания. Сторона этого прямоугольника равна катету прямоугольного треугольника, образованного основанием и высотой усеченной пирамиды. Для нахождения катета (a) воспользуемся теоремой Пифагора:
a^2 + a^2 = (2a)^2
2a^2 = 4a^2
a^2 = 4a^2 - 2a^2
a^2 = 2a^2
Разделим обе части на a^2:
1 = 2
Это неверное утверждение.
Таким образом, мы попали в противоречие, и у нас нет значения для стороны прямоугольника и, следовательно, не можем вычислить его площадь.
2. Однако, мы можем вычислить площадь двух прямоугольных треугольников на боковых гранях. Эти треугольники образуют угол 45 градусов с плоскостью основания. Для этого мы можем воспользоваться формулой площади треугольника: S = 0.5 * a * b * sin(C), где a и b - длины двух катетов, а C - угол между ними.
В данной задаче, длина катета a равна стороне основания а, и длина катета b равна стороне основания 2a. Искомым углом С будет угол между катетом а и катетом 2a, который равен 45 градусам.
Для первого треугольника:
S1 = 0.5 * a * a * sin(45°) = 0.5 * a^2 * sin(45°)
Для второго треугольника:
S2 = 0.5 * 2a * a * sin(45°) = a^2 * sin(45°)
Теперь сложим площади этих двух треугольников, чтобы получить площадь боковой поверхности:
S = S1 + S2 = 0.5 * a^2 * sin(45°) + a^2 * sin(45°)
S = 1.5 * a^2 * sin(45°)
Таким образом, площадь боковой поверхности усеченной пирамиды равна 1.5 * a^2 * sin(45°). Это будет ответ на задачу.