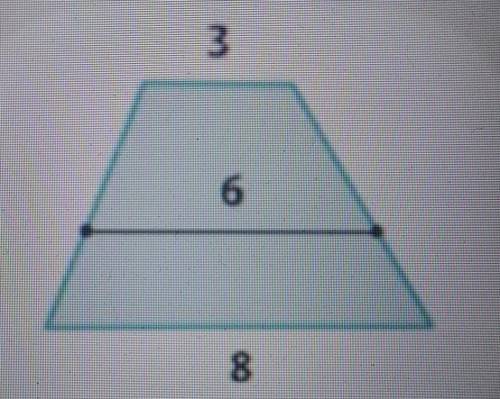
Основание трапеции равны 3 и 8. Отрезок с концами на её боковых сторонах параллелен основаниями и имеет длину 6. В каком отношении его концы делят боковые стороны трапеции?

Добрый день! Буду рад помочь вам разобраться с этим математическим вопросом. Чтобы решить эту задачу, нам нужно использовать свойства параллельных линий и подобия треугольников. Первым шагом давайте обозначим буквами длины сегментов нашей трапеции. Пусть AB = 3, CD = 8, AE = x и BF = y, как на рисунке. Мы знаем, что AB || CD, поэтому треугольники ADE и BFC подобны. По свойству подобных треугольников, отношения соответствующих сторон равны. То есть: \(\frac{AE}{BF} = \frac{AD}{BC} = \frac{AD + CD}{BC + CD}\) Теперь заметим, что BC + CD = AB, так как BC + CD + DE + AE = AB + DE + AE, и DE + AE = BF. Подставим значения: \(\frac{x}{y} = \frac{AB + CD}{AB} = \frac{8+3}{3} = \frac{11}{3}\) Таким образом, концы отрезка делят боковые стороны трапеции в отношении 11:3. Надеюсь, я максимально подробно разъяснил решение данной задачи. Если у вас возникнут еще вопросы, я с удовольствием отвечу на них.