Основание трапеции, около которой можно описать окружность, равны 4 см и 14 см, а одна из боковых сторон равна 13 см.найдите длину описаной окружности
Другие вопросы по теме Геометрия
Популярные вопросы
- На рисунке AB=BC угол 1=130 градусов. Найдите угол 2...
1 - Тема нравственного эгоизма в «Экспонат №…»...
2 - Составить монолог на тему Моя школьная жизнь , используя бессоюзные сложные...
1 - Мое впечатление от знакомства с писателем Самойловым кратко...
1 - Определить координаты вершины...
3 - Запиши число, если 1/8 его часть равна 10 А) 80 б) 18 в) 800...
1 - Задание 2. Вычислите и напишите, чему будут равняться следующие выражения....
3 - Определить условия постановки тире во 2, 3-м предложениях графически. Фиалка-символ...
2 - Ромео и Джульетта впечатления 10 предложений но не из интернета наругают...
3 - Частица участвует одновременно в двух гармонических колебаниях, происходящих...
2
Трапеция АВСД является равнобедренной, т.к. окружность описать можно только вокруг равнобедренной трапеции. Значит, АВ=СД=13 см.
Проведем высоты ВН и СК. Тогда НК=ВС=4 см, АН=КД=(14-4):2=5 см.
Рассмотрим ΔАВН - прямоугольный. ВН=√(АВ²-АН²)=√(169-25)=√144=12 см.
Рассмотрим ΔАВД и найдем его площадь:
S=1\2 * АД * ВН= 1\2 * 14 * 12=84 см².
Из ΔВДН найдем ВД по теореме Пифагора ВД=√(ВН²+ДН²)=√(144+81)=√225=15 см
Найдем радиус окружности, описанной вокруг ΔАВД (этим же радиусом описана окружность вокруг трапеции АВСД)
R =(АВ*ВД*АД)/(4*S)=13*15*14\4*84=8,125 см
Найдем длину окружности по формуле С=2πR=2π*8,125=16,25π см
ответ: 16,25π см.
Из прямоугольного треугольника ABE найдем BE по т. Пифагора
Из треугольника ABD найдем диагональ BD по т. Косинусов
Вписанный угол измеряется половинной дуги, на которую он опирается.
Прямая является касательной к окружности тогда и только тогда, когда радиус, проведенной в точку касания, перпендикулярен ей, то есть
BF - высота, медиана и биссектриса равнобедренного треугольника BOD
Синус - отношение противолежащего катета к гипотенузе, т.е.
Длина окружности: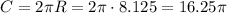 см
см