1. Геометрия
  2. Основание прямой призмы-прямоугольный

Основание прямой призмы-прямоугольный треугольник с гипотенузой с и астрым углом альфа.диагональ боковой грани, содержащей катет,протеволежащий углу альфа, наклонена к пл-сти основания под углом бета.найдитеобъём призмы.

ddosanov777 ddosanov777    1   21.03.2019 03:00    3

Ответы
маруська62 маруська62  26.05.2020 11:47

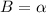Пусть ABCA_1B_1C_1  - данная пряммая призма с основанием ABC (прямоугольным треугольником с пряммым углом С), AB=c, угол B=\alpha;

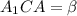
угол A_1CA=\beta

 

Катеты треугольника АВС равны

b=AC=AB*sin B=c*sin \alpha;\\a=BC=AB*cos B=c*cos \alpha

Высота призмы равна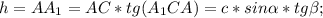 h=AA_1=AC *tg (A_1CA)=c*sin \alpha * tg \beta;

 

Площадь основания равна

S=\frac{ab}{2}=\frac{c*sin \alpha *c*cos \alpha}{2}=\frac{c^2*2sin \alpha *cos \alpha}{4}=\frac{c^2*sin(2\alpha)}{4}

 

Обьем призмы равен

V=Sh=\frac{c^2*sin(2\alpha)}{4} * c*sin \alpha * tg \beta=\frac{c^3*sin(2\alpha)sin \alpha *tg \beta}{4}


Основание прямой призмы-прямоугольный треугольник с гипотенузой с и астрым углом альфа.диагональ бок
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
nurmuh4med nurmuh4med  28.08.2019 17:10
Впараллелограмме abcd диагональ ac в 2 раза больше стороны ab и ∠acd = 74°. найдите угол между диагоналями параллелограмма. ответ дайте в град...
ЯСоваНоТупая ЯСоваНоТупая  30.03.2021 11:00
Розв язання. Нехай задано три відрізки a, bic (мал. 414). Треба побудувати трикутник ABC, у якого BC = а,AC = b, AB = с.​...
Aliya205 Aliya205  30.03.2021 10:59
Знайдіть кут при вершині рівнобедреного трикутника, якщо кут при вершині в 3 рази більший за кут при основі​...
ansarildar ansarildar  30.03.2021 10:58
знайдіть координати середини відрізку AB, якщо A(-2;5;4), B(2;0;7)...
Lagunahey Lagunahey  30.03.2021 10:57
решить контрольную на тему Сумма углов треугольника 7 класс...
Glek11 Glek11  30.03.2021 10:57
дуже треба . Як можна зрозуміліше . ів....
лулу36 лулу36  30.03.2021 10:56
1. Знайдіть координати середини відрізка АВ, якщо: 1) А(2; -11; 0), B(4; -7; 6); 2) А(-2; 5; 4), В(2; 0; 7).2. Знайдіть довжину відрізка CD, якщо:1) C(4; 0; -1), D(2; 3; 5);...
nastya123litvin nastya123litvin  30.03.2021 10:56
в треугольнике АВС проведена биссектриса AL. Угол АВС равен 110°, угол АLС равен 135°. Найдите угол ВАС​...
vadar22222 vadar22222  30.03.2021 10:56
1. Знайдіть координати середини відрізка АВ, якщо: 1) А(2; -11; 0), B(4; -7; 6); 2) А(-2; 5; 4), В(2; 0; 7).2. Знайдіть довжину відрізка CD, якщо:1) C(4; 0; -1), D(2; 3; 5);...
ученик11111023531 ученик11111023531  24.04.2021 23:38
РЕШИТЬ 7. Периметр ромба дорівнює 20 см, сума довжин його діагоналей дорівнює 14 см. Знайдіть площу ромба (у см 2 ). 8. Знайдіть площу прямокутної трапеції (у см 2 ), в якої...

Популярные вопросы