Основание прямоугольного параллелепипеда ABCDA1B1C1D1 - квадрат ABCD со стороной 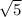см, длина ребра АА1 = 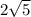. Найдите площадь сечения, проведенного через точки C,P и M, где P - середина AD и M - середина ВВ1 .

Чтобы найти площадь сечения, проведенного через точки C, P и M в прямоугольном параллелепипеде, нам нужно использовать знания о геометрии фигуры.

Шаг 1: Найдем координаты точек C, P и M.
Так как основание параллелепипеда - квадрат ABCD, мы знаем, что точка C имеет координаты (0,0,0).
Также, так как P - середина стороны AD, координаты точки P можно найти, используя среднее арифметическое координат концов стороны AD. Первоначально, найдем координаты точки A:
x_A = 0
y_A = 0
z_A = a, где a - длина ребра квадрата ABCD.
Теперь найдем координаты точки D:
x_D = a
y_D = 0
z_D = 0
Используя эти координаты, найдем координаты точки P:
x_P = (x_A + x_D)/2 = (0 + a)/2 = a/2
y_P = (y_A + y_D)/2 = 0/2 = 0
z_P = (z_A + z_D)/2 = a/2 + 0 = a/2
Теперь найдем координаты точки M, используя среднее арифметическое координат концов стороны BB1.
Найдем сначала координаты точки B:
x_B = 0
y_B = a
z_B = 0
Теперь найдем координаты точки B1:
x_B1 = 0
y_B1 = a
z_B1 = a
Используя эти координаты, найдем координаты точки M:
x_M = (x_B + x_B1)/2 = (0 + 0)/2 = 0
y_M = (y_B + y_B1)/2 = (a + a)/2 = 2a/2 = a
z_M = (z_B + z_B1)/2 = (0 + a)/2 = a/2

Таким образом, мы получили координаты точек C (0,0,0), P (a/2,0,a/2) и M (0,a,a/2).

Шаг 2: Найдем уравнение плоскости, проходящей через точки C, P и M.
Чтобы найти уравнение плоскости, проходящей через данные точки, мы можем использовать формулу плоскости, которая имеет вид Ax + By + Cz + D = 0, где A, B, C и D - коэффициенты, которые мы должны найти.

Заметим, что все точки лежат на одной плоскости, поэтому коэффициенты этой плоскости можно найти путем подставления координат всех точек в уравнение плоскости и решения системы уравнений.
Подставив координаты точки C (0,0,0), получаем:
0A + 0B + 0C + D = 0
D = 0

Подставив координаты точки P (a/2,0,a/2), получаем:
(a/2)A + 0B + (a/2)C + D = 0
(a/2)A + (a/2)C = 0
A + C = 0 (1)

Подставив координаты точки M (0,a,a/2), получаем:
0A + aB + (a/2)C + D = 0
(a/2)C + D = -aB
C + 2D = -2B (2)

Теперь у нас есть два уравнения (1) и (2) с двумя неизвестными A, B, C и D, и мы можем решить систему уравнений для нахождения этих неизвестных коэффициентов.

Шаг 3: Найдем площадь сечения, проведенного через точки C, P и M.
Так как плоскость, проходящая через эти точки, задается уравнением Ax + By + Cz + D = 0, площадь сечения будет зависеть от коэффициентов A, B и C.

Площадь сечения можно найти, используя формулу площади сечения, когда уравнение плоскости записано в виде Ax + By + Cz + D = 0. В данном случае, площадь сечения будет равна |(BC)|, где вектор BC - векторное произведение векторов B и C.

Так как мы нашли коэффициенты A = 1, B = 2, C = -1 и D = 0 в предыдущем шаге, эти значения будут также коэффициентами уравнения плоскости, проходящей через точки C, P и M.
Подставив значения A, B и C в формулу для нахождения площади сечения, получаем:
|(BC)| = |(1,-2,-1)| = √(1^2 + (-2)^2 + (-1)^2) = √(1 + 4 + 1) = √6

Таким образом, площадь сечения, проведенного через точки C, P и M, равна √6 квадратных сантиметров.