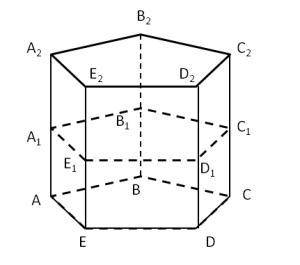
Основание призмы — правильный пятиугольник со стороной 6 см. Длина её бокового ребра — 16 см. Плоскость сечения проведена через середины боковых рёбер. Найди:
1. результирующий вектор 2⋅EE1−→−−+E1A1−→−−−D2A2−→−−+0,5⋅D2D−→−− —
2. Его длину

Добрый день! Рад видеть тебя в классе! Давай решим задачу по нахождению результирующего вектора и его длины.

Перед тем, как начать, давай разберемся с некоторыми основными понятиями.

Первое, что нам нужно знать, это как вычислить вектор. Вектор - это направленный отрезок, который характеризуется своей длиной и направлением. В обозначениях вектор обычно обозначается стрелочкой над буквой, например, вектор AB обозначается как →AB.

Теперь перейдем к решению задачи. У нас есть следующие векторы: 2EE1→−−+E1A1→−−−D2A2→−−+0,5D2D→−−. Нам нужно найти их результирующий вектор и его длину.

Шаг 1: Начнем с вектора EE1→. В данной задаче не указаны точные значения точек и расстояний, поэтому мы будем работать с относительными значениями.

Если посмотреть на рисунок, то можно заметить, что вектор EE1→ и вектор E1A1→ имеют одинаковую длину, так как эти отрезки являются одной и той же стороной пятиугольника. Таким образом, можно записать вектор EE1→ как 2⋅E1A1→.

Теперь у нас остался только вектор 2⋅E1A1→. Мы можем его вычислить следующим образом:

2⋅E1A1→ = 2⋅(EA→ + AE1→)

Поскольку мы знаем, что длина стороны пятиугольника равна 6 см, мы можем записать:

EA→ = 6 см

Также, по условию, длина бокового ребра пятиугольника равна 16 см. Это означает, что AE1→ = 16 см.

Теперь мы можем подставить эти значения в формулу и вычислить вектор 2⋅E1A1→:

2⋅E1A1→ = 2⋅(6 см + 16 см)

2⋅E1A1→ = 2⋅22 см

2⋅E1A1→ = 44 см

Таким образом, результирующий вектор 2⋅EE1→−−+E1A1→−−−D2A2→−−+0,5D2D→−− равен 44 см.

Шаг 2: теперь давай найдем длину этого вектора. Для этого нужно использовать формулу длины вектора, которая выглядит следующим образом:

Длина вектора = √(x^2 + y^2 + z^2)

Где x, y, и z - это координаты вектора. В нашем случае, у нас нет конкретных координат, поэтому мы будем использовать только длину вектора.

Длина вектора EE1→−−+E1A1→−−−D2A2→−−+0,5D2D→−− равна √(44^2) = √1936 = 44 см.

Таким образом, длина результирующего вектора 2⋅EE1→−−+E1A1→−−−D2A2→−−+0,5⋅D2D−→−− равна 44 см.

Надеюсь, это решение помогло тебе разобраться в задаче. Если возникнут еще вопросы, не стесняйся задавать!