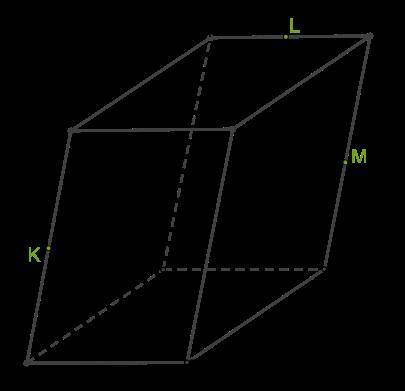
Основание параллелепипеда — прямоугольник. Точки K, L и M — середины векторов AA1, B1C1 и CC1 соответственно. Двугранный угол при ребре AB равен 60°. AB= 9, BC= 12. CL является высотой грани BB1C1C. Грань BB1C1C перпендикулярна основанию параллелепипеда.
Найди:
1. Длину вектора B1C−→−−
2. Длину вектора AD1−→−−
(Где необходимо — округли ответ до сотых.)
Другие вопросы по теме Геометрия
Популярные вопросы
- В емкостью 0,5 м3 находится азот при температуре 30 0С и избыточном...
2 - Даны двугранный угол алфа a бетта и точки А, В, С, D, где А, В€ а,...
1 - 10. Яка маса розчину оцтової кислоти прореагує з 13 г цинку, якщо...
2 - Кто правил после Олега Князя...
1 - Кто знает что такое гинирировантие...
1 - Напиши мне 5 предложений на широкую и на узкую тему...
3 - В таблице указано содержание витаминов (в миллиграммах) в 100 гфруктов....
3 - Який архітектурний ордер використали стародавні майстри....
2 - Представители импресионизма модерн символизма импресионизма пастимресионизма...
2 - Период басынан аяғына қарай бейметалдық қасиет қалай өзгереді...
2
1. Длина вектора B1C−→−− :
Мы знаем, что точка L - середина вектора B1C1. По свойству параллелограмма, вектор BL−→−− будет равен вектору B1C−→−−, так как вектор B1C−→−− это диагональ параллелограмма.
Теперь рассмотрим грань ABCB1 параллелепипеда. Она является прямоугольным треугольником AB1C со смежными катетами AB и ACB1.
Известно, что AB = 9 и BC = 12. Мы можем использовать пифагорову теорему для нахождения длины гипотенузы ACB1:
ACB1 = √(AB^2 + BC^2) = √(9^2 + 12^2) = √(81 + 144) = √225 = 15.
Таким образом, длина вектора B1C−→−− равна 15.
2. Длина вектора AD1−→−− :
Мы можем использовать тот же треугольник ABCB1, чтобы найти длину вектора AD1−→−−. Заметим, что AD1−→−− это высота треугольника ABCB1, и по определению высоты, она перпендикулярна стороне BC.
Мы уже нашли длину гипотенузы ACB1, которая равна 15, и знаем, что двугранный угол при ребре AB равен 60°. Так как BC = 12, то у нас есть прямоугольный треугольник с гипотенузой ACB1 = 15 и катетом BC = 12.
Теперь мы можем использовать тригонометрическую функцию синус для нахождения длины высоты AD1−→−−:
sin(60°) = BC/ACB1
sin(60°) = 12/ACB1
ACB1 = 12/sin(60°) = 12/√3 = 4√3.
Таким образом, длина вектора AD1−→−− равна 4√3 (округлено до сотых).