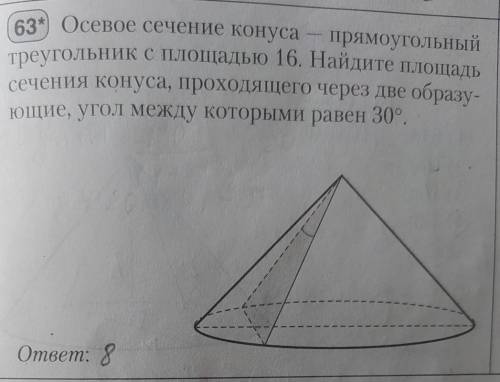
Осевое сечение конуса -прямоугольный треугольник с площадью 16. Найдите площадь сечения конуса , проходящего через две образующее , угол между которым равен 30°. Если возможно , то объяснение с рисунком . ​

Для решения данной задачи, нам потребуется использовать знания о геометрии и свойствах конусов.

Дано, что осевое сечение конуса представляет собой прямоугольный треугольник с площадью 16.

Давайте обозначим:
- одну из образующих конуса за "l";
- другую образующую конуса, образующую угол 30° с первой образующей, за "h";
- высоту конуса (перпендикулярную к основанию конуса и проходящую через вершину осевого сечения) за "H";
- стороны прямоугольного треугольника осевого сечения конуса за "a" и "b".

Нам известно, что площадь осевого сечения конуса равна 16:

S_осевого сечения = 16

Площадь осевого сечения конуса равна половине произведения катетов прямоугольного треугольника:

S_осевого сечения = (1/2) * a * b

Из уравнения выше мы можем найти выражение для одного из катетов, например, a:

a = (2 * S_осевого сечения) / b

Также, у нас есть информация о том, что угол между образующими конуса равен 30°. Используя геометрические свойства прямоугольных треугольников, мы можем записать равенство:

tan(30°) = a / b

Значение тангенса угла 30° равно:

tan(30°) = 1 / sqrt(3)

Теперь мы можем заменить a в уравнении выше:

1 / sqrt(3) = (2 * S_осевого сечения) / b

Решим это уравнение относительно b:

b = (2 * S_осевого сечения) / (1 / sqrt(3))
= 2 * S_осевого сечения * sqrt(3)

Таким образом, мы нашли выражение для b.

Чтобы найти площадь сечения конуса, проходящего через две образующие, угол между которыми равен 30°, нам нужно найти площадь треугольника, образованного этим сечением.

Площадь треугольника равна половине произведения катетов:

S_сечения = (1/2) * a * b

Теперь, подставим значения a и b:

S_сечения = (1/2) * [(2 * S_осевого сечения) / b] * b
= S_осевого сечения

Таким образом, площадь сечения конуса, проходящего через две образующие, угол между которыми равен 30°, равна 16.

В рисунке, обозначим через "l" первую образующую, через "h" вторую образующую, образующую угол 30° с первой образующей, через "a" и "b" стороны прямоугольного треугольника осевого сечения конуса. Нарисуем треугольник и обозначим высоту конуса "H". Подписи под рисунком.

- На рисунке:
основание конуса - прямоугольный треугольник ABC;
точка D - вершина осевого сечения;
AD - первая образующая l;
BD - вторая образующая h;
точка F - высота конуса H.

F
/ | \
/ | \
/ | \
C‾‾|__‾‾‾__‾‾‾B
A D
l h

- В данном рисунке, CD - гипотенуза прямоугольного треугольника ABC.
Площадь осевого сечения равна площади этого треугольника, то есть S_осевого сечения = (1/2) * AB * AF = 16.

Зная площадь осевого сечения, мы можем найти размеры этого треугольника.
Одна из формул для площади треугольника: S_осевого сечения = (1/2) * AB * AF.
Подставим известное нам значение площади и найдем значение длины стороны AB (можно принять за "a").

(1/2) * AB * AF = 16

AB * AF = 32

Зная площадь и одну из сторон равностороннего треугольника, мы можем найти вторую сторону:

AF = AB * sqrt(3)/2, так как угол между основанием и высотой треугольника равен 60°.

Подставим значение AF в уравнение и найдем AB:

AB * AB * sqrt(3)/2 = 32

AB^2 = 64 * 2 / sqrt(3)

AB^2 = 128 / sqrt(3)

AB = sqrt(128 / sqrt(3))

- Теперь, когда мы знаем стороны треугольника, мы можем рассчитать площадь конусного сечения:

Сначала найдем длину BD, применив теорему косинусов для прямоугольного треугольника ABD:

BD^2 = AD^2 + AB^2 - 2 * AD * AB * cos(30°)

BD = sqrt(AD^2 + AB^2 - 2 * AD * AB * cos(30°))

Подставим значения и найдем BD:

BD = sqrt(l^2 + (128 / sqrt(3)))

Теперь посчитаем площадь сечения конуса, проходящего через две образующие:

S_сечения = (1/2) * l * BD

S_сечения = (1/2) * l * sqrt(l^2 + (128 / sqrt(3)))

Таким образом, площадь сечения конуса, проходящего через две образующие, угол между которыми равен 30°, равна (1/2) * l * sqrt(l^2 + (128 / sqrt(3))).

Заметим, что в данном выражении нет переменной h, так как она не влияет на площадь осевого сечения.

Для получения численного ответа вам необходимо знать значение l и подставить его в выражение выше.