1. Геометрия
  2. Определите вид треугольника,

Определите вид треугольника, стороны которого равны 8 см, 15 см, 17 см

Ал923к Ал923к    3   01.04.2021 16:37    7

Ответы
Катя132211111 Катя132211111  01.05.2021 16:40

Формула вычисления углов треугольника — зная все стороны: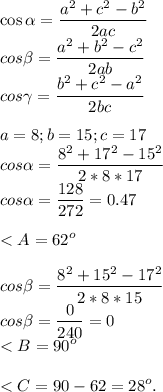 \displaystyle\\\cos\alpha = \frac{a^2+c^2-b^2}{2ac}\\cos\beta = \frac{a^2+b^2-c^2}{2ab}\\cos\gamma = \frac{b^2+c^2-a^2}{2bc}\\\\a = 8; b = 15; c = 17\\cos\alpha = \frac{8^2+17^2-15^2}{2*8*17}\\cos\alpha = \frac{128}{272} = 0.47\\\\

Вид треугольника — прямоугольный.

ПОКАЗАТЬ ОТВЕТЫ
asya343434 asya343434  01.05.2021 16:40

ответ: Это прямоугольный треугольник

Гипотенуза = 17 см

1катет= 15 см

2 катет= 8см

Объяснение: 17в квадратных см = 8 в квадратных см + 15 в квадратных см 289=289 объясняет нам, что этот треугольник прямоугольный.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Петья Петья  11.09.2019 21:30
Найдите меньшую высоту треугольника со сторонами 24 25 7...
Дошик58694 Дошик58694  11.09.2019 21:30
Дано abcd прямоугольник, af биссектриса угла bad, определите вид треугольника abf и его углы....
Баумгертнер Баумгертнер  11.09.2019 21:30
Точки a, c, m и p лежат в плоскости альфа,а точка b не принадлежит альфа.постройте точку пересечения прямой mp с плоскостью abc.поясните....
айфон66666 айфон66666  12.05.2020 15:48
Довжина відрізка АВ дорівнює 4 см.На відрізку взято точки М і К так,що АМ:МК:КВ=1:2:3.Знайдіть довжину відрізка МК....
mklslajh mklslajh  12.05.2020 15:47
Сторона треугольника равна 12 см а проведенная к ней высота 3 см найдите площадь треугольника ​...
ksusha20032 ksusha20032  28.02.2019 07:50
Втреугольнике авс ,mn-средняя линия, m принадлежит ав, n принадлежит bc. доказать что треугольник mbn подобен треугольнику abc =)...
KOBPAHET KOBPAHET  28.02.2019 07:50
1.сторона ромба равна 10, а один из его углов равен 30 нградусам. найдите радиус окружности, вписанной в ромб. 2.найдите больший угол треугольника, если две его стороны видны...
Arina200444 Arina200444  28.02.2019 07:50
.(Впрямоугольном треугольнике dce с прямым углом с проведена биссектриса ef причем fc=13 см. найдите расстояние от точки f до прямой de)....
Juliana2414 Juliana2414  28.02.2019 07:50
Стороны треугольнка равны 3 см, 2 см и корень имз 3 см. определите вид этого треугольника....
Uliana7003 Uliana7003  28.02.2019 07:50
Вравнобедренном треугольнике авс угол в=120 градусов, о-точка пересечения биссектрис. окружность радиуса 2 корня из 3 см вписана в этот в этот треугольник и касается прямых...

Популярные вопросы