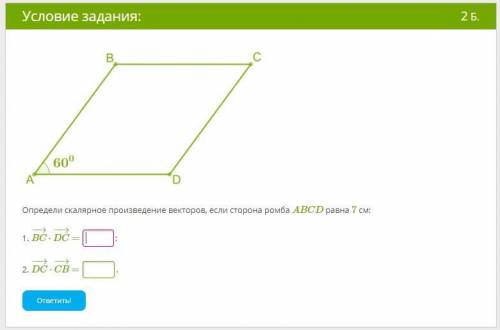
Определи скалярное произведение векторов, если сторона ромба ABCD равна 7 см:

Скалярное произведение векторов - это число, которое равно произведению длин этих векторов на косинус угла между ними.

В данном случае, чтобы определить скалярное произведение векторов, нам нужно найти длины этих векторов и угол между ними.

Для начала, нам нужно определить длину вектора AB. По условию, сторона ромба ABCD равна 7 см. Так как ABCD - ромб, то вектор AB является диагональю ромба и делит его на два равных треугольника. Таким образом, длина вектора AB равна половине длины диагонали ромба.

Для нахождения длины диагонали ромба, мы можем использовать теорему Пифагора. В ромбе все стороны равны, поэтому мы можем взять один из углов и использовать его для прямоугольного треугольника. В данном случае, мы можем взять угол A. Используя теорему Пифагора, мы можем записать:

AC^2 = AB^2 + BC^2

Так как сторона ромба ABCD равна 7 см, мы можем заменить BC на 7 и получить:

AC^2 = AB^2 + 7^2

Далее, мы можем заменить AB на половину длины диагонали, то есть на AC/2:

(AC/2)^2 = (AC/2)^2 + 7^2

Теперь мы можем решить это уравнение относительно AC. Раскрывая скобки, мы получаем:

AC^2/4 = AC^2/4 + 49

Умножив обе части уравнения на 4, мы получаем:

AC^2 = AC^2 + 196

Отсюда мы видим, что AC^2 сократятся, и мы получаем 0 = 196. Это противоречие, так как невозможно, чтобы ноль равнялся 196.

Из этого мы можем сделать вывод, что данная фигура не является ромбом. Таким образом, в заданном рисунке невозможно определить скалярное произведение векторов.