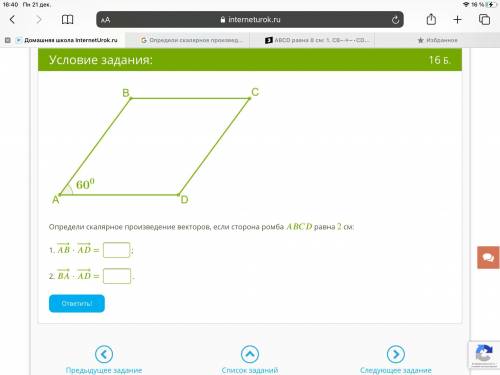
Определи скалярное произведение векторов, если сторона ромба равна 2 см:

1. −→−⋅−→− = ;

2. −→−⋅−→− = .

Для определения скалярного произведения векторов, мы должны знать их координаты или длины векторов и угол между ними.

Для удобства, давайте обозначим точки на диаграмме следующим образом: точка A (верхний левый угол ромба), точка B (верхний правый угол ромба), точка C (нижний правый угол ромба) и точка D (нижний левый угол ромба).

Поскольку сторона ромба равна 2 см, мы можем считать, что каждый из векторов AB, BC, CD и DA имеет длину 2 см.

Теперь рассмотрим первый вопрос:
1. −→−⋅−→− = ?
Мы должны определить скалярное произведение векторов AB и CD.

Зная, что каждый из этих векторов имеет длину 2 см, мы можем сказать, что их длины одинаковы. Кроме того, векторы AB и CD ориентированы в разные стороны, то есть они противоположны друг другу.

Скалярное произведение векторов определяется по формуле:
−→−⋅−→− = |−→−| * |−→−| * cos(θ),
где |−→−| обозначает длину вектора, а θ представляет собой угол между векторами.

Поскольку векторы AB и CD имеют одинаковую длину и направлены в противоположных направлениях, угол между ними составляет 180 градусов.

Таким образом, скалярное произведение векторов AB и CD равно:
−→AB⋅−→CD = |−→AB| * |−→CD| * cos(180°).

Так как длина вектора AB и CD равна 2 см, формула будет выглядеть следующим образом:
−→AB⋅−→CD = 2 * 2 * cos(180°).

Для решения этого уравнения, нам понадобится значение косинуса 180 градусов.
Косинус 180 градусов равен -1.

Подставляем значение косинуса и решаем уравнение:
−→AB⋅−→CD = 2 * 2 * (-1) = -4.

Ответ на первый вопрос: −→−⋅−→− = -4.

Теперь рассмотрим второй вопрос:
2. −→−⋅−→− = ?

Мы должны определить скалярное произведение векторов BC и DA.
Аналогично первому вопросу, векторы BC и DA имеют длину 2 см и они ориентированы в разные стороны.

Угол между этими векторами также составляет 180 градусов.

Используя формулу для скалярного произведения векторов и рассуждения аналогичные предыдущему вопросу, мы можем найти его значение:

−→BC⋅−→DA = 2 * 2 * cos(180°) = -4.

Ответ на второй вопрос: −→−⋅−→− = -4.

Таким образом, ответ на оба вопроса равен -4.