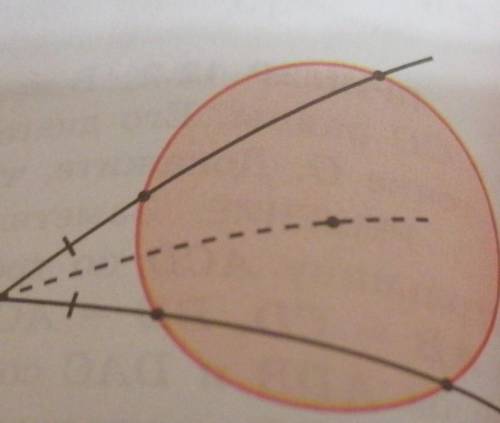
окружность пересекают стороны угла в четырех точках оказалось что две из них находятся на равном расстоянии от его вершины. Докажите что центр этой окружности лежит на биссектрисе данного угла

Объяснение:

окружность пересекают стороны угла в четырех точках оказалось что две из них находятся на равном

Проведем хорду BC.

Центр окружности O лежит на серединном перпендикуляре к хорде BC.

Вершина A равнобедренного △BAC лежит на серединном перпендикуляре к основанию BC.

То есть прямая AO является серединным перпендикуляром к BC.

В равнобедренном треугольнике серединный перпендикуляр к основанию является биссектрисой.

AO - биссектриса угла A.

Давайте разберемся сначала в том, что значит "биссектриса угла". Биссектрисой угла называется луч, который делит данный угол пополам. В данном случае, биссектриса угла AOB будет лучак OC.

Определение задачи говорит нам, что окружность пересекает стороны угла AOB в четырех точках - A, B, C и D. Из этих четырех точек две находятся на равном расстоянии от вершины угла O, то есть точки A и B находятся на равном отдалении от точки O.

Нам нужно доказать, что центр этой окружности лежит на биссектрисе угла AOB. Для этого нам потребуется использовать некоторые свойства окружностей и углов.

Для начала, давайте построим радиусы OA и OB и соединим их с центром окружности O. Также построим луч OC, который является биссектрисой угла AOB.

Теперь вспомним некоторые свойства окружностей. Как известно, радиус окружности перпендикулярен к хорде, которой он является. В нашем случае, радиусы OA и OB перпендикулярны к соответствующим хордам AC и BD.

Далее, у нас есть две хорды (AC и BD), которые находятся на равном расстоянии от точки O. Это значит, что эти хорды находятся на одинаковом расстоянии от центра окружности O.

Используя это свойство окружностей, мы можем заключить, что точки C и D находятся на одинаковом расстоянии от O. Это означает, что луч OC и луч OD одинаковой длины.

Теперь, обратите внимание на треугольники AOC и BOD. У нас есть два равных угла: угол AOC и угол BOD, так как они соответствующие углы при пересечении параллельных линий AC и BD биссектрисой OC. У нас также есть общий угол O - угол при вершине обоих треугольников.

Исходя из этих равенств, мы можем сделать заключение, что треугольники AOC и BOD равны по двум углам и общей стороне OC. Следовательно, они равны по всему.

Следовательно, сторона AO равна стороне BO (так как они являются радиусами окружности), и треугольники AOB и BOA также равны.

Заключительный шаг в доказательстве - мы знаем, что треугольники AOB и BOA равны, поэтому их медианы (лучи, исходящие из вершины треугольника и проходящие через центрократный ему) также равны. В этом случае, луч OC будет медианой треугольника ABO и будет проходить через центр окружности.

Таким образом, мы доказали, что центр окружности лежит на биссектрисе угла AOB.