Один из острых углов прямоугольного треугольника равен 60°, а сумма короткого катета и гипотенузы равна 9 см.определи длину короткого катета. найти: 1. величина второго острого угла равна ° 2. длина короткого катета равна см.

1. Сумма углов тр-ка равно 180. Один прямой (90), а второй - 60.
180-90-60=30.
2. Есть такое правило - катет, лежащий напротив угола 30 градусов, равен половине гипотенузы. Значит гипотенуза равно 6, а маленький катет 3.
Всего добрго ;*

Свойство острых углов прямоугольного треугольника: сумма острых углов прямоугольного треугольника равна 90°.

Свойство катета, лежащего против угла в 30°: катет, лежащй против угла в 30°, равен половине гипотенузы.

Против меньшего угла лежит меньшая сторона, а против меньшей стороны лежит меньший угол.

Поэтому:

1. Втрой острый угол равен: 90° - 60° = 30°.

2. Значит, против угла в 30° лежит меньший катет.

   Обозначим меньший катет х см, тогда гипотенуза будет равна (2х) см. Т.к. по условию задачи их сумма равна 9 см, то состаим и решим уравнение:

х + 2х = 9,

3х = 9,

х = 9 : 3,

х = 3.

Значит, меньший катет прямоугольного треугольника равен 3 см.

ответ: 1. 30°. 2. 3 см.

Дано :

ΔАВС — прямоугольный (∠С = 90°).

∠А = 60°.

АВ + короткий катет = 9 см.

Найти :

∠В = ?

Короткий катет = ?

В прямоугольном треугольнике сумма острых углов равна 90°.

Следовательно, ∠А + ∠В = 90° ⇒ ∠В = 90° - ∠А = 90° - 60° = 30°.

В треугольнике против меньшего угла лежит меньшая сторона.

Так как ∠В — самый меньший угол в ΔАВС, то АС (катет, лежащий напротив этого угла) самая меньшая сторона, соответственно и есть короткий катет.

Тогда нам нужно найти АС.

В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузы.

Следовательно, АС =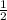 *АВ или АВ = 2*АС.

Составим уравнение —

АВ + АС = 9 см

2*АС + АС = 9 см

3*АС = 9 см

АС = 3 см.

30° ; 3 см.