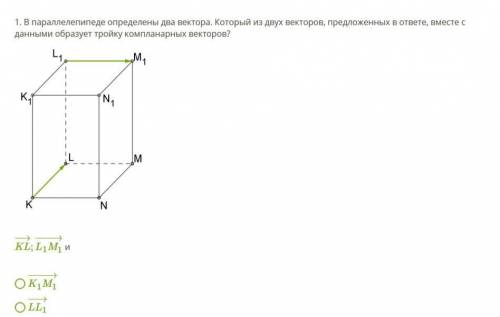
ОЧЕНЬ В параллелепипеде определены два вектора. Который из двух векторов, предложенных в ответе, вместе с данными образует тройку компланарных векторов?
KL, L1M1 и
1) К1М1
2) LL1
Другие вопросы по теме Геометрия
Популярные вопросы
- Отметь × словочетания в которых есть сущ., 1-го скл в форме ед.ч р.п залез...
1 - Составте сложное предложение со словом причина...
3 - Чому в одісеї гомера ми тільки і п ятій пісні зустрічаємося з головним...
1 - Найдите корень уравнения! каждая строчка-- это новое уравнение (d+7) :...
2 - Сделайте глагольные и именные словосочетания со словами притворщик и заранее...
2 - Сочинение, один самый интересный день на море...
3 - Сколько двухзначных чисел из цифр 0 2 4 6 если цифры в записи числа не...
3 - Как сделать деревянную кормушку по плану?...
1 - Сто нужно вставить в предложение a funny crocodile have got или has got...
3 - Решите не могу решить а(а: 10),если а 0 в(17: b),если b 0 c(-c; 5) ,если...
2
Вектор - это направленный отрезок прямой, который имеет длину и направление. Векторы могут суммироваться (сложение) и умножаться на число (умножение на скаляр).
Два вектора называются компланарными, если они лежат в одной плоскости или параллельны друг другу. Векторы, образующие компланарную тройку, могут быть выражены через линейные комбинации друг друга.
Теперь рассмотрим данную задачу. Нам дан параллелепипед и два вектора KL и L1M1 внутри него. Нам нужно определить, который из двух предложенных векторов, К1М1 или LL1, будет компланарен с данными векторами KL и L1M1.
Для этого нам необходимо понять, как связаны векторы KL, L1M1 и К1М1 или LL1. Для этого мы можем использовать свойства параллелепипеда.
В параллелепипеде противоположные ребра параллельны и равны по длине. Это значит, что вектор KL будет параллельным вектору К1М1, так как KL и К1М1 - это противоположные ребра параллелепипеда.
Таким образом, вектор KL будет компланарен с вектором К1М1.
Теперь рассмотрим вектор LL1. Если мы внимательно рассмотрим параллелепипед, то заметим, что вектор LL1 - это диагональ (вектор, соединяющий противоположные вершины). Векторы KL и L1M1 являются ребрами параллелепипеда и не являются диагональными.
Таким образом, вектор LL1не будет компланарен с данными векторами KL и L1M1.
Итак, для данной задачи, единственный вектор, предложенный в ответе и вместе с данными векторами KL и L1M1 образующий тройку компланарных векторов, является вектор К1М1 (ответ 1).
Надеюсь, это решение понятно для вас. Если у вас есть ещё вопросы или что-то непонятно, не стесняйтесь спрашивать!