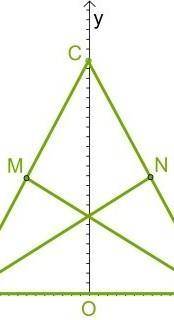
Очень ! В координатной системе находится равнобедренный треугольник ABC (AC=BC). Проведены медианы AN и BM к боковым сторонам треугольника. Длина стороны AB = 4, а высоты CO = 16.
Определи координаты вершин треугольника, координаты точек M и N и длину медиан AN и BM (oтвет округли до сотых).
A( )?
B( )?
C( )?
N( )?
M( )?
AN=
BM=
​

Пусть начало координат в точке А. Тогда А(0;0)

И сторона AB расположена по направлению оси ОХ. Тогда, так как АВ=14, то B(14;0).

Высота СО делит АВ пополам. Значит, С(7;0). И, так как длина этой высоты 20, то С(7;20).

Точка N - Середина стороны СВ. Чтобы найти координаты середины, нужно вычислить среднее арифметическое координат концов отрезка.

N((14+7)/2;(20+0)/2)=N(10.5;10).

Аналогично считаем M:

M((7+0)/2;(20+0)/2)=M(3.5;2.).

Чтобы найти длины медиан, сначала найдём координаты векторов. И, так как AC=BC, то достаточно посчитать только AN.

Чтобы найти координаты вектора, надо от координат конца отнять координаты начала:

AN(10.5-0;10-0)=AN(10.5;10)

Чтобы найти длину вектора, надо посчитать корень из суммы квадратов координат(теорема Пифагора)

|AN|=√(10,5^2+10^2)=√210.25=14.5

Объяснение: