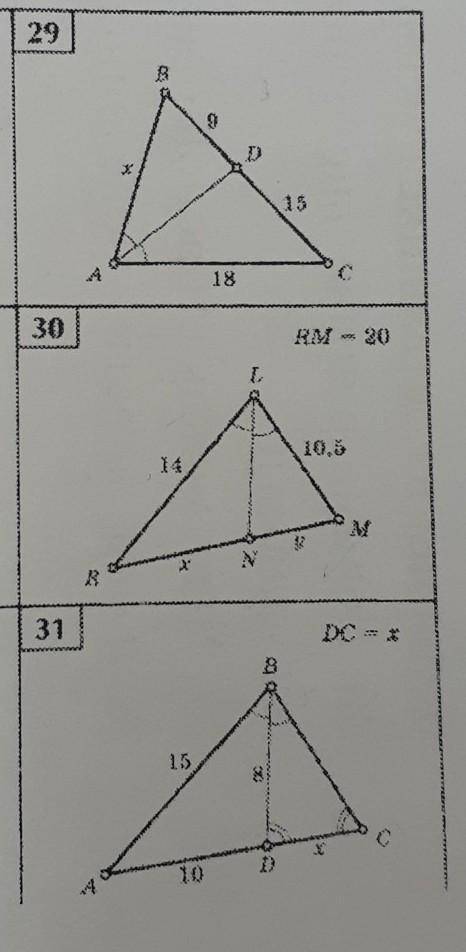
очень надо, не получается.​

А30

Конечно, я готов выступить в роли школьного учителя и объяснить вам данный вопрос.

На изображении приведена задача математического характера. Для ее решения вам понадобится знать как работать с длиной и шириной прямоугольника, а также как найти его периметр и площадь. Давайте разберем задачу пошагово:

1. Анализ задачи:
Нам нужно найти площадь прямоугольника на картинке. На картинке не указаны значения длины и ширины, но мы имеем информацию о периметре равном 66 единицам.

2. Определение формул:
Периметр прямоугольника рассчитывается по формуле: P = 2 * (a + b), где a и b - длина и ширина прямоугольника. Для нахождения площади прямоугольника нам понадобится формула: A = a * b.

3. Установление значений:
Пусть длина прямоугольника равна a, а ширина равна b. Заметим, что в формулах периметра и площади не имеет значения, какую из сторон мы назовем длиной, а какую шириной. Можно выбрать любую из сторон для дальнейших расчетов.

4. Решение задачи:
Поскольку у нас задан периметр прямоугольника равный 66, мы можем записать уравнение:
66 = 2 * (a + b)

С помощью этого уравнения мы можем выразить одну переменную через другую:
a + b = 33

Мы также имеем формулу для площади прямоугольника:
A = a * b

Теперь мы хотим выразить площадь через только одну переменную. Можно, например, выразить ширину (b) через длину (a) с помощью уравнения a + b = 33:
b = 33 - a

Подставим это значение в формулу для площади:
A = a * (33 - a)

Из этого уравнения мы можем получить квадратное уравнение:
A = 33a - a^2

Таким образом, площадь прямоугольника равна функции A = 33a - a^2.

5. Решение квадратного уравнения:
Для нахождения максимального значения площади, нам необходимо найти вершину параболы, заданной уравнением A = 33a - a^2. Вершина параболы находится по формуле a = -b/(2a) в квадратном уравнении Ax^2 + Bx + C = 0.

В нашем случае, A = -1, B = 33 и C = 0. Подставим эти значения в формулу:
a = -33/(2*(-1))
a = -33/(-2)
a = 16.5

Таким образом, длина прямоугольника равна 16.5. Зная это, мы можем найти ширину прямоугольника:
b = 33 - 16.5
b = 16.5

Теперь мы можем найти площадь прямоугольника:
A = 16.5 * 16.5
A = 272.25

Итак, площадь прямоугольника на картинке равна 272.25.

Надеюсь, что объяснение было понятным и помогло вам решить данную задачу. Если у вас возникнут еще вопросы, не стесняйтесь задавать.