ОЧЕНЬ
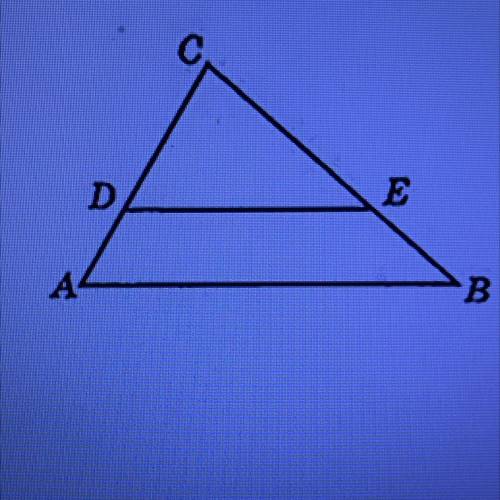
на рисунке AC=8 AB=12 CD=6 угол ABC равен углу DEC найдите DE

Для решения этой задачи нам потребуется знание о геометрических свойствах треугольников.

Дано: на рисунке дан треугольник ABC, в котором AC = 8, AB = 12 и CD = 6. Угол ABC равен углу DEC. Требуется найти длину отрезка DE.

Чтобы найти длину отрезка DE, мы можем использовать свойство подобных треугольников. В данном случае мы можем заметить, что треугольники ABC и DEC подобны.

Почему они подобны? Поскольку угол ABC равен углу DEC, а по свойству подобных треугольников, если углы одного треугольника равны углам другого треугольника, то эти треугольники подобны.

Теперь перейдем к пошаговому решению:

Шаг 1: Заметим, что треугольник ABC и треугольник DEC имеют две одинаковые стороны: AC = 8 и CD = 6.

Шаг 2: Используем пропорцию сторон треугольников ABC и DEC. Поскольку треугольники ABC и DEC подобны, то отношение длин сторон будет одинаково:
AC / DE = AB / CD

Шаг 3: Подставим известные значения:
8 / DE = 12 / 6

Шаг 4: Упростим пропорцию:
8 / DE = 2

Мы можем упростить пропорцию, разделив обе части на 2:

4 / DE = 1

Шаг 5: Проведем обратную операцию, возведение в степень, чтобы избавиться от деления:
DE = 4

Итак, длина отрезка DE равна 4.