Обьем конуса равен 3. Найдите обьем вписанного в конус правильной четырехугольной пирамиды.
ответы:
а) 6/пи
в) 4/пи
с)
д) 8/пи
е) 9/пи
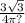
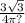
Другие вопросы по теме Геометрия
Популярные вопросы
- Дописати 3 речення про косю у коси не було друзив кожоного ранку вин...
1 - Составить 10 предложений со словом make или его формой made...
2 - По заданным координатам (x,y,z) определить положение точки в пространстве...
3 - Перевести текст на язык самостоятельно без переводчика...
2 - Учитель , что из себя представляет (чему и как учит и т. п.) ...
1 - К300 мл 20% раствора серной кислоты ( p= 1, 14 г/мл) прилили 250 мл...
2 - 8класс на первом фото текст, а на втором слова которые надо вставить...
1 - Как изменится магнитный поток, пронизывающий замкнутый контур, если...
2 - Определите общее число молекул ,находящихся в 7,15л оксида серы 4,при...
3 - Выбери словосочетания с деепричастиями. накатываясь на берег, получить...
1
ответ: а) 6/π
Пусть H – высота конуса и высота пирамиды, R – радиус основания конуса и радиус описанной около основания пирамиды окружности. Найдем отношение объема вписанной пирамиды к объему конуса.
Объём конуса, и объём пирамиды вычисляются по формуле:
V = 1/3 Sосн·Н
Так как в основании конуса – круг, то Sосн. конуса = πR²
Так как по условию четырехугольная пирамида правильная, то в основании – квадрат, следовательно Sосн. пирамиды = а²
Vп/Vк = 1/3 а²H / 1/3πR²H = а² / πR²
Площадь квадрата равна половине квадрата длины его диагонали:
S = d²/2, d = 2R, S = (2R)²/2 = 2R², тогда:
Vп/Vк = а² / πR² = 2R² / πR² = 2/π
Так как по условию задачи объём конуса равен 3, то Vп/3 = 2/π, Vп = 6/π
ответ: 6/π