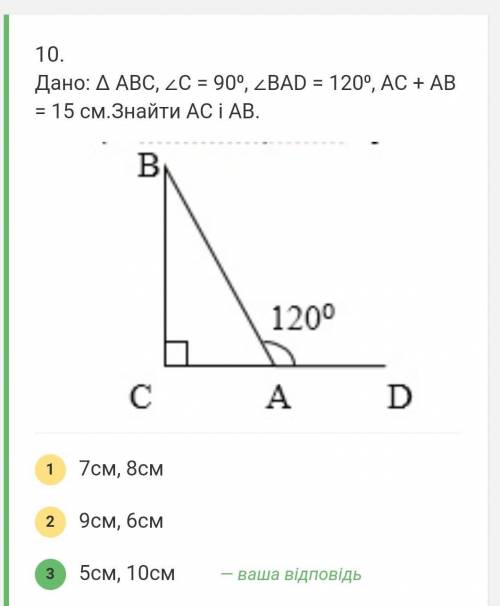
объясните как нашли это,я не понимают
Другие вопросы по теме Геометрия
Популярные вопросы
- Какие государства боролись за контроль над Балтийским морем в 17 веке?...
3 - Составьте формулы двух гомологов и двух изомеров для вещества:...
2 - Написати продовження Злочин і кара...
2 - решить, будут ответы не по теме забаню...
1 - В прямоугольную трапецию вписана окружность. Точка ка- сания окружности...
3 - «Эпоха Просвещения. Время преобразований». Укажите десять наиболее важных...
3 - поясніть, з якими негативними проявами у громадському житті боровся герой...
3 - Как река Погромка изменяется в разные времена года?...
3 - Определи длительность «года» (один оборот вокруг Солнца) на планетах и...
1 - Установите соответствие между видом движения шарика и соотношением еговеса...
1
Объяснение:
1) ∠BAD и ∠BAC - смежные, поэтому их сумма = 180°. Следовательно,
∠BAC = 180° - ∠BAD = 180° - 120° = 60°
2) Рассмотрим △АВС, он прямоугольный, т.к. ∠С =90°.
∠BAC = 60°. Т.к., сумма углов △-ка = 180°, то
∠СВА = 180° - 90° - 60° = 30°
3) Известно, что катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы,т.е.
АС = ½АВ, но по условию
АС + АВ =15см или
½АВ + АВ = 15 (см)
1,5АВ = 15
АВ = 15 : 1,5 =10 (см)
Соответственно, АС = ½АВ = 10/2 =5 (см)
ответ:
Объяснение:∠BAD -- внешний угол тр.-ка при вершине А
Он является смежным с ∠ВАС . Тогда ∠ВАС= 180°-120°= 60°
В прямоугольном тр-ке если один острый угол равен 60°, то
другой острый равен 30°.° Извесно, что катет , лежащий против
угла в 30° равен половине гипотенузы.
в тр-ен АВС АВ + АС =15 см. Две части приходится на гипотенузу а
одна часть на катет АС. Поэтому 15 : 3 =5 - это длина катета АС
а 5×2= 10 см - это длина гипотенузы АВ. ответ 5см и 10 см