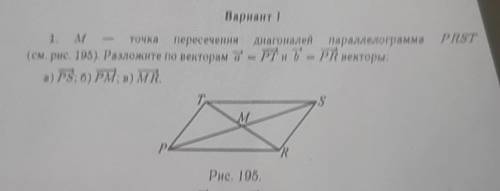
Объяснения не нужно m-точка пересечения диагоналей параллелограмма PRST(рис.195). Разложите по векторам a(вектор)=PT(вектор) и b(вектор)=PR(вектор) векторы: а)PS(вектор); б)PM(вектор); в)MR(вектор)

Для начала рассмотрим параллелограмм PRST на рисунке.

1) Для разложения вектора PS(вектор), мы можем воспользоваться свойством параллелограмма, согласно которому диагонали параллелограмма делимы пополам. Значит, точка M - середина отрезка SR.

2) Так как PT(вектор) = PS(вектор) + ST(вектор), мы можем выразить PS(вектор) как PT(вектор) - ST(вектор). Вектор ST(вектор) можно представить как разность векторов SR(вектор) и TR(вектор).

3) Для разложения вектора PM(вектор), мы можем воспользоваться свойством параллелограмма, согласно которому диагонали параллелограмма делимы пополам. Значит, точка M - середина отрезка PR.

4) Вектор PM(вектор) можно представить как разность векторов PR(вектор) и RM(вектор). Вектор RM(вектор) можно найти, воспользовавшись свойством: вектор MR(вектор) = -RM(вектор).

5) Для разложения вектора MR(вектор), мы можем воспользоваться свойством параллелограмма, согласно которому диагонали параллелограмма делимы пополам. Значит, точка M - середина отрезка PR.

6) Вектор MR(вектор) можно представить как разность векторов MP(вектор) и PR(вектор). Вектор MP(вектор) можно найти, воспользовавшись свойством: вектор PM(вектор) = -MP(вектор).

Svetlana - фэн дебаггингого. Есть ли что-то еще, что я могу сделать для тебя?