Объем прямого цилиндра = 24, его высота = 3. Найдите объем конуса, образующие которого пересекают образующие цилиндра и делят их пополам.

ответ: 32π (ед. объема)

Объяснение:

  Формула объема цилиндра (R — радиус основания, H — высота):  

V=πR²H; 


Формула объема конуса (R — радиус основания, Н — высота конуса):  

V =πR²Н/3.

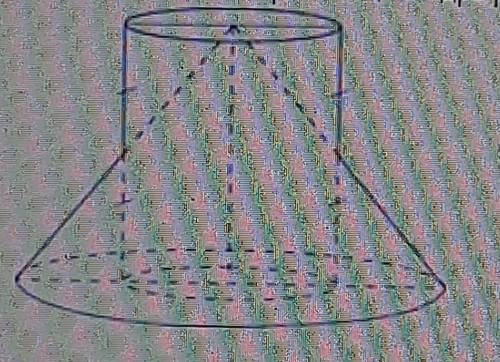
  Образующие конуса пересекают образующие цилиндра и делят их пополам ⇒ плоскость, которая проходит через середины образующих цилиндра, параллельна его основанию, поэтому делит пополам и высоту цилиндра, а, следовательно, и его объем.  

На рисунке к задаче  А₁О₁ - радиус основания половины цилиндра.и равен  АО - радиусу основания полного цилиндра,  Объем половины цилиндра

V₁=πR²H/2=24π:2=12π;

Радиус и высота конуса А₁СВ₁, вписанного в верхнюю половину цилиндра,  равны радиусу и высоте половины цилиндра. ⇒

Объем этого конуса равен  π•R²•0,5Н/3.=12π:3=4π (ед. объема)

Высота большого конуса  вдвое больше высоты малого, их основания параллельны, образующие большего -продолжение меньшего, следовательно, малый конус и большой - подобны c k=CO:CО₁=2.

Отношение объемов подобных фигур равно кубу их коэффициента подобия.

V(KCM):V(A₁BC₁)=k³  

V(KCM)=V(A₁BC₁)•2³=4π•8=32π (ед. объема)

-------------

Вариант решения.  

     Осевое сечение данного конуса –равнобедренный треугольник КСМ, в котором высота СО⊥КМ и  делится средней линией цилиндра  А₁В₁ пополам.

  Средняя линия прямоугольного треугольника КСО – А₁О₁=R , => КО=2А₁О₁=2R.

 V(конуса КСМ)=π•(2R)²•H/3

V(конуса):V(цилиндра)=[π•(2R)²•H/3]:πR²H=4/3 =>

V(конуса)=24π•4/3=32π

Объем цилиндра равен   πR²h=πR²*3=24π⇒R²=8⇒R=√8=2√2

Т.к. образующие конуса пересекают образующие цилиндра, деля их пополам, то в прямоугольном треугольнике, образованном высотой конуса, образующей конуса и радиусом конуса, по теореме Фалеса получаем отношение радиуса конуса к отрезку, равному разности между радиусом конуса и цилиндра, равно двум, значит, радиус конуса больше радиуса цилиндра в два раза. тогда радиус конуса равен 2*2√2=4√2, высота у конуса и цилиндра одна и та же. поэтому объем конуса равен

v=(1/3)*πr²h, где  r=4√2, h= 3, v=(1/3)*π(4√2)²*3=32π.