1. Геометрия
  2. Объем цилиндра, вписанного

Объем цилиндра, вписанного в куб равен 2п. какова поверхность сферы, описанного около этого куба?

Сириc Сириc    3   21.05.2019 03:20    1

Ответы
Vica73751 Vica73751  14.06.2020 23:41

Пусть а - ребро куба. Объем цилиндра: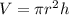 V=\pi r^2h

Для вписанного в данный куб цилиндра получим:

r=a/2, h=a. тогда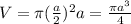   V=\pi (\frac{a}{2})^2a=\frac{\pi a^3}{4}

\frac{\pi a^3}{4}=2\pi 

a^3=8

a=2

Диагональ d данного куба является диаметром описанной сферы.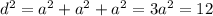d^2=a^2+a^2+a^2=3a^2=12

 d=2\sqrt3

Радиус сферы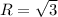 R=\sqrt3

Поверхность сферы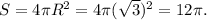 S=4\pi R^2=4\pi (\sqrt3)^2=12\pi.

 

ответ: 12П.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Bereke2006 Bereke2006  13.07.2019 17:00
Дано abcd-ромб; угол d=45 найти: площадь...
sonya0013 sonya0013  13.07.2019 16:50
Внешний угол при вершине m треугольника mnk равен 120 стороны mn=3см, mk=8см...
lari133 lari133  13.07.2019 16:50
100 , кто ! в треугольнике abc отрезок bd является биссектрисой угла b равного 120 градусов. найти отрезки cd, если известно, что bc=10 и bd=1. полностью решение...
topovychuvak topovychuvak  13.07.2019 16:50
Из точки м проведены к плоскости альфа перпендикуляр мо=12см и наклонная мq=13см.через q проведена в плоскости альфа прямая а, перпендикулярная mq. найдите расстояние между прямыми...
andrei271 andrei271  13.07.2019 16:50
Счем с связана низкая соленость вод гвинейского залива...
katkovakatsluЛпл katkovakatsluЛпл  13.07.2019 16:50
Вычислить координаты вершины с равностороннего треугольника авс, если даны координаты а(-9,10), в(-1,4) (должно получится 2 точки,только как? )...
2006marusya 2006marusya  13.07.2019 16:50
Дано a b c треугольника bd меньше ac в 2 раза площадь равна 64 сантиметров в квадрате найти ac...
Gorki2005 Gorki2005  13.07.2019 16:50
Найдите площадь равнобедренного треугольника если боковая сторона равна 7 сантиметров основания 4 найдите высоту равнобедренной трапеции с основанием 6 сантиметров и 14 и если боковая...
reginailt reginailt  13.07.2019 16:50
Найдите площадь равнобедренного треугольника если боковая сторона равна 7 сантиметров основания 4...
NoxchiKent NoxchiKent  13.07.2019 16:50
Решить за 8-ой класс, и подробно расписать решить надо вот что: : 1)высота bd треугольника abc делит основание ac на отрезки: ad=8см, dc=12 см,а угол а при основании равен 45°. найдите...

Популярные вопросы