Обчислити площу фігури, обмежену лініями у = 2– х, у = х 2
Другие вопросы по теме Геометрия
Популярные вопросы
- УЖЕ ТРЕТИЙ РАЗ ЗАДАЮ ОДИН И ТОТ ЖЕ ВОПРОС Составьте уравнения реакций, соответствующие...
1 - Морфологический разбор неопределённого местоимения. (Не)когда они были товарищами...
2 - Які особливості характерні для популярної музики ?...
2 - C: X-0Y-50Z-50B:X-50Y-25Z-80А:Х-120У-90Z-10Ось Х направлена влево, ось У...
1 - Я люблю смотреть Склифосовского ...
3 - Robert Pattinson 1) in the romantic-fantasy Twilight. Itwas 2) by CatherineHardwicke....
2 - Спросите у близких, какие виды ремесел изображены на картинках...
3 - напишите правильный ответ в тетради...
1 - сам толком не могу разобраться надеюсь на вашу Две задачи решить...
1 - Рід Рюриковичів до 1300 р....
2
Приравняем данные функции и решим полученное квадратное уравнение:
Найдём площадь по формуле Ньютона-Лейбница:
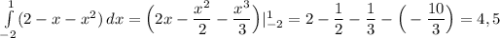
ответ: