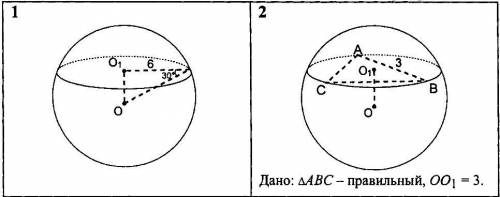
О- центр шара, О1 и О2 _центры кругов – сечений шара плоскостью. Найти площадь поверхности шара.

треуг. О1ОК (уг О1=90°)
син 30°= ОО1/6
ОО1=6×син30°=3 см
ОК²=ОО1²+О1К²
ОК²=9+36=45
ОК=4кор5
R=45

Чтобы найти площадь поверхности шара, нам потребуется использовать формулу для расчета площади поверхности:

S = 4πr^2,

где S - площадь поверхности, а r - радиус шара.

Для начала, нам нужно найти радиус шара. Мы знаем, что О - это центр шара, а O1 и O2 - центры кругов, которые являются сечениями шара плоскостью. Таким образом, O1 и O2 представляют собой точки на поверхности шара.

Мы можем использовать расстояние между О и O1 (или О2), чтобы найти радиус шара. Поскольку O1 и O2 находятся на поверхности шара, их расстояние до О будет равно радиусу шара.

Теперь нам нужно вычислить расстояние между О и O1 (или О2). Для этого можно применить теорему Пифагора:

OO1^2 = O1O2^2 + O2O^2.

OO1^2 - это расстояние между O и O1, O1O2^2 - это расстояние между O1 и O2, а O2O^2 - это расстояние между O2 и O.

У нас есть информация о расстоянии между O1 и O2, которое равно 20 м, поэтому можем заменить O1O2^2 в формуле:

OO1^2 = 20^2 + O2O^2.

Следующим шагом будет вычисление расстояния O2O, которое является радиусом шара.
Поскольку O1 и O2 являются центрами кругов и сечениями шара, диаметры этих кругов будут равны рассматриваемым расстояниям OO1 и O1O2. Это означает, что радиус O2O равен 20/2 = 10 м.

Теперь мы можем заменить O2O^2 в формуле:

OO1^2 = 20^2 + 10^2.

OO1^2 = 400 + 100.

OO1^2 = 500.

Вычислив значение для OO1^2, мы можем найти OO1:

OO1 = √500.

OO1 = 10√5 м.

Таким образом, радиус шара r = 10√5 м.

Используя формулу для расчета площади поверхности шара, мы можем подставить значение радиуса и рассчитать площадь:

S = 4πr^2.

S = 4π(10√5)^2.

S = 4π(100 * 5).

S = 4π * 500.

S = 2000π.

Ответ: площадь поверхности шара равна 2000π.