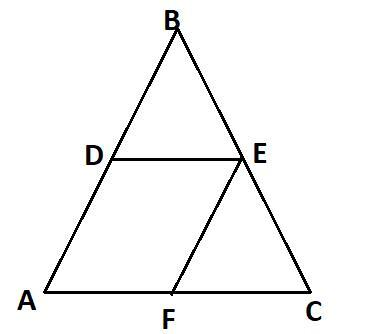
НУЖНО СДЕЛАТЬ СЕГОДНЯ!На рисунке в равносторонем треугольнике ABC со стороной 4см проведены среднии линии DE и EF. Укажите : а) векторы одинаково направленные с вектором DE б) векторы противоположно направленные к вектору CB.

Добрый день!

Чтобы ответить на данный вопрос, нам понадобится немного знаний о треугольниках и векторах.

У нас задан равносторонний треугольник ABC со стороной 4 см. Равносторонний треугольник - это треугольник, у которого все стороны равны между собой.

На рисунке проведены средние линии DE и EF. Средняя линия это линия, соединяющая середины двух сторон треугольника. В данном случае, DE соединяет середину стороны AB с серединой стороны AC, а EF - середину стороны AC с серединой стороны BC.

Чтобы найти векторы, одинаково или противоположно направленные относительно вектора DE, нам необходимо рассмотреть направления этих векторов и сравнить их.

Для начала, найдем вектор DE. Для этого нужно взять конечную точку вектора E и вычесть из нее начальную точку вектора D. Начальная точка вектора D - это конечная точка вектора C, а конечная точка вектора E - начальная точка вектора E.

Таким образом, вектор DE можно найти, вычтя координаты начальной точки из координат конечной точки. В нашем случае, начальная точка вектора D имеет координаты (0, 0), а конечная точка вектора E - (2, 4). Вычтем первую координату начальной точки из первой координаты конечной точки, и вторую координату начальной точки из второй координаты конечной точки:
Для x-координаты: 2-0 = 2
Для y-координаты: 4-0 = 4

Итак, вектор DE имеет координаты (2, 4).

Теперь мы можем рассмотреть другие векторы и сравнить их с вектором DE.

В нашем случае, векторы EF и CB пересекаются в одной точке, это значит, что они образуют угол между собой.

1) Для векторов, одинаково направленных с вектором DE, нужно обратить внимание на направление этих векторов. Если они направлены в том же направлении, что и вектор DE, то они считаются одинаково направленными. Векторы будут одинаково направленными, если они будут направлены в одну и ту же сторону относительно вектора DE.

На рисунке видно, что вектор EF направлен в сторону AB, а вектор DE направлен в сторону BC. Они направлены в разные стороны, поэтому мы не можем сказать, что вектор EF одинаково направлен с вектором DE.

2) Для векторов, противоположно направленных к вектору CB, мы должны обратить внимание на направление этих векторов. Если они направлены в противоположную сторону относительно вектора CB, то они считаются противоположно направленными этому вектору.

Опять же, из рисунка видно, что вектор EF направлен от стороны AB к стороне AC (в противоположную сторону от стороны CB). Таким образом, мы можем сказать, что вектор EF противоположно направлен к вектору CB.

Таким образом, ответ на вопрос:
а) Ни один из векторов на рисунке не одинаково направлен с вектором DE.
б) Вектор EF противоположно направлен к вектору CB.

Надеюсь, что данное объяснение помогло вам понять решение этой задачи. Если у вас возникнут еще вопросы - с удовольствием помогу!