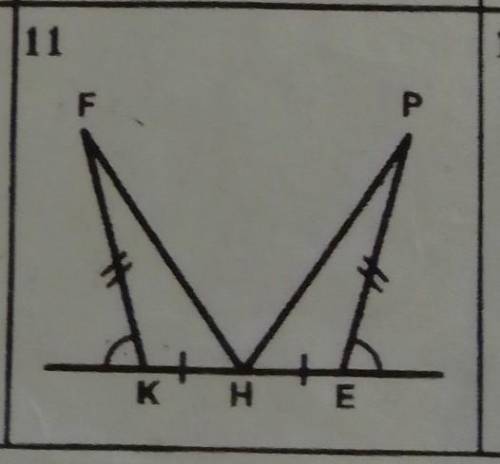
Нужно доказать равенство
Задача 7 класса
Другие вопросы по теме Геометрия
Популярные вопросы
- Простите, а сколько надо раз надо поливать маргаритки ИМЕННО пани зося? ...
2 - Укажите найьильший десятковий дроб з дома цифрами писля коми який меньший вид...
3 - Запиши частное в виде смешанного числа:348:23=...
1 - 2. Установите соответствие между уровнем организации живых организмов и их характеристикойвень...
1 - Topic 2. Creativity 1) Do you like musіс? 2) Why do you like it? 3) ...
2 - Продовжте речення за змістом: «Мальовничу пейзажну картину, що блищить «полив...
2 - вы должны прям написать это ответить на, а потом на б и остальные, кто не так...
3 - Выберите правильный ответ We saw James ... 1.ago two months 2.a year ago 3.in...
3 - 2. Вычисли. 171.4-329-2317.3 + 15.2840 : (956 - 948)900 - 269.3 + 193954: 6...
1 - Функция спроса на яблоки имеет следующий вид: Qd=20-2p, где Qd-величина спроса...
3
\(\frac{4}{a+b} + \frac{9}{a-b} = \frac{13}{a^2 - b^2}\)
можно воспользоваться методом приведения дробей к общему знаменателю и последующим сокращением. Давайте разберемся, как это сделать.
Шаг 1: Найдем общий знаменатель для дробей \(\frac{4}{a+b}\) и \(\frac{9}{a-b}\). Общим знаменателем будет произведение знаменателей данных дробей. Таким образом, общий знаменатель равен \((a+b)(a-b)\).
Шаг 2: Приведем к общему знаменателю обе дроби:
\(\frac{4}{a+b} = \frac{4(a-b)}{(a+b)(a-b)}\)
\(\frac{9}{a-b} = \frac{9(a+b)}{(a+b)(a-b)}\)
Шаг 3: Теперь сложим полученные дроби:
\(\frac{4(a-b)}{(a+b)(a-b)} + \frac{9(a+b)}{(a+b)(a-b)} = \frac{4(a-b)+9(a+b)}{(a+b)(a-b)}\)
Шаг 4: Упростим числитель дроби:
\(4(a-b) + 9(a+b) = 4a-4b+9a+9b = 13a+5b\)
Шаг 5: Подставим полученный числитель в общую дробь:
\(\frac{13a+5b}{(a+b)(a-b)} = \frac{13a+5b}{a^2-b^2}\)
Шаг 6: Сравниваем полученную дробь с исходным равенством:
\(\frac{13a+5b}{a^2-b^2}\)
Мы видим, что дроби совпадают, следовательно, исходное равенство верно:
\(\frac{4}{a+b} + \frac{9}{a-b} = \frac{13}{a^2 - b^2}\).
Таким образом, равенство доказано.