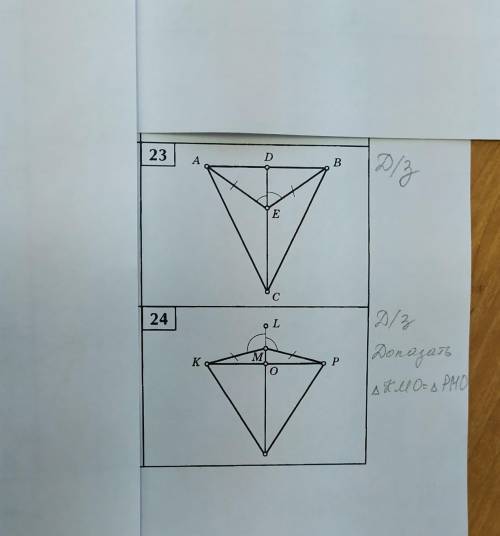
нужно доказать, что треугольники равны
Другие вопросы по теме Геометрия
Популярные вопросы
- Составить 10 предложений на , на тему...
1 - Скиньте самую известную классику, для школьного выступления надо; )...
3 - Запишете в виде суммы тригонометрических функций выражение a)sin5a-cos2a b)cos6a*cos(-15a)...
2 - Кданным именам существительным подберите имена сущ.близкие по значению неправда.друг.путь.метель.труд.холод.доктор...
1 - Охарактеризовать влияние удобрений на экологичность продуктов питания....
1 - Построй два прямоугольника с одинаковой площадью, равной 12см в квадрате.какова...
2 - Каких поэтов вы знаете? и кто знает больше 10 поэтов? ....
1 - Почему у материка только одна крайняя точка? (антарктида)...
2 - Вертолет предали расстоянии 3150 километров час 7: 00 за сколько часов вертолет...
1 - 10 в каждый казахской семье име..тся домбра. какие удивительные мелодии звуч..т...
1
Эти треугольники прямоугольные (MO⊥KP), поэтому чтобы доказать их равенство нам нужны только 2 пары соответственно равных элементов
1). ∠KML = ∠ LMP (по условию), ∠KML смежный с ∠KMO, ⇒ ∠KMO = 180° - ∠KML, ∠PMO смежный с ∠LML, ⇒ ∠PMO = 180° - ∠PML, так как ∠KML = ∠ LMP, то можно сказать, что ∠PMO = 180° - ∠KML, ⇒ ∠KMO = ∠PMO
2). Рассмотрим ΔKMO и ΔPMO:
KM = PM (по условию)
∠KMO = ∠ PMO (по доказанному)
следовательно ΔKMO = ΔPMO (гипотенузе и острому углу)
(KM и MP гипотенузы, потому что лежать напротив прямого угла)
чтд